Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T03:21:51.548Z Has data issue: false hasContentIssue false
  • English
  • Français

The local cyclicity problem: Melnikov method using Lyapunov constants

Part of: Smooth dynamical systems: general theory Qualitative theory

Published online by Cambridge University Press:  19 April 2022

Luiz F. S. Gouveia Open the ORCID record for Luiz F. S. Gouveia [Opens in a new window]  and
Joan Torregrosa Open the ORCID record for Joan Torregrosa [Opens in a new window]
Luiz F. S. Gouveia
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Spain Departamento de Matemática, Universidade Estadual Paulista, 15054-000 São José do Rio Preto, Brazil ([email protected]; [email protected])
Joan Torregrosa
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Spain Centre de Recerca Matemàtica, Campus de Bellaterra, 08193 Bellaterra, Barcelona, Spain ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1991, Chicone and Jacobs showed the equivalence between the computation of the first-order Taylor developments of the Lyapunov constants and the developments of the first Melnikov function near a non-degenerate monodromic equilibrium point, in the study of limit cycles of small-amplitude bifurcating from a quadratic centre. We show that their proof is also valid for polynomial vector fields of any degree. This equivalence is used to provide a new lower bound for the local cyclicity of degree six polynomial vector fields, so $\mathcal {M}(6) \geq 44$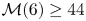. Moreover, we extend this equivalence to the piecewise polynomial class. Finally, we prove that $\mathcal {M}^{c}_{p}(4) \geq 43$ 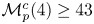and $\mathcal {M}^{c}_{p}(5) \geq 65.$

Keywords

Melnikov theoryLyapunov constantslocal cyclicity

MSC classification

Primary: 34C07: Theory of limit cycles of polynomial and analytic vector fields (existence, uniqueness, bounds, Hilbert's 16th problem and ramifications)
Secondary: 34C23: Bifurcation 37C27: Periodic orbits of vector fields and flows
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 2 , May 2022 , pp. 356 - 375
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acary, V., Bonnefon, O. and Brogliato, B., Nonsmooth modeling and simulation for switched circuits, Lecture Notes in Electrical Engineering, Volume 69 (Springer, Dordrecht, 2011).CrossRefGoogle Scholar
Andronov, A. A., Vitt, A. A. and Khaikin, S. E., Theory of oscillators (Pergamon Press, Oxford-New York-Toronto, Ontario, 1966).Google Scholar
Andronov, A. A., Leontovich, E. A., Gordon, I. I. and Maĭer, A. G., Theory of bifurcations of dynamic systems on a plane (Halsted Press [A division of John Wiley & Sons], New York-Toronto, Ontario, 1973). Israel Program for Scientific Translations, Jerusalem-London.Google Scholar
Arnol'd, V. I., Loss of stability of self-oscillations close to resonance and versal deformations of equivariant vector fields, Funct. Anal. Appl. 11(2) (Apr 1977), 85–92.CrossRefGoogle Scholar
Bautin, N. N., On the number of limit cycles which appear with the variation of coefficients from an equilibrium position of focus or center type, American Math. Soc. Translation 1954(100) (1954), 19.Google Scholar
di Bernardo, M., Budd, C. J., Champneys, A. R. and Kowalczyk, P., Piecewise-smooth dynamical systems, Applied Mathematical Sciences, Volume 163 (Springer-Verlag London, Ltd., London, 2008). Theory and applications.Google Scholar
Blows, N. and Lloyd, T. R., The number of limit cycles of certain polynomial differential equations, Proc. Roy. Soc. Edinburgh Sect. A 98(3-4) (1984), 215–239.CrossRefGoogle Scholar
Bondar, Y. L. and Sadovskiĭ, A. P., On a theorem of Zoladek, Differ. Uravn. 44(2) (2008), 263–265.Google Scholar
Buică, A., On the equivalence of the Melnikov functions method and the averaging method, Qual. Theory Dyn. Syst. 16(3) (2017), 547–560.CrossRefGoogle Scholar
Buică, A. and Llibre, J., Averaging methods for finding periodic orbits via Brouwer degree, Bull. Sci. Math. 128(1) (2004), 7–22.CrossRefGoogle Scholar
Buzzi, C., Pessoa, C. and Torregrosa, J., Piecewise linear perturbations of a linear center, Discrete Contin. Dyn. Syst. 33(9) (2013), 3915–3936.CrossRefGoogle Scholar
Castillo, J., Llibre, J. and Verduzco, F., The pseudo-Hopf bifurcation for planar discontinuous piecewise linear differential systems, Nonlinear Dynam. 90(3) (2017), 1829–1840.CrossRefGoogle Scholar
Chicone, C. and Jacobs, M., Bifurcation of limit cycles from quadratic isochrones, J. Diff. Eq. 91(2) (1991), 268–326.CrossRefGoogle Scholar
Christopher, C., Estimating limit cycle bifurcations from centers. In Differential equations with symbolic computation, Trends Math., pp. 23–35. (Birkhäuser, Basel, 2005).CrossRefGoogle Scholar
Cima, A., Gasull, A., Mañosa, V. and Mañosas, F., Algebraic properties of the Lyapunov and period constants, Rocky Mountain J. Math. 27(2) (1997), 471–501.CrossRefGoogle Scholar
Cima, A., Gasull, A. and Mañosas, F., A note on the Lyapunov and period constants, Qual. Theory Dyn. Syst. 19 (2020), 4.CrossRefGoogle Scholar
Coombes, S., Neuronal networks with gap junctions: a study of piecewise linear planar neuron models, SIAM J. Appl. Dyn. Syst. 7(3) (2008), 1101–1129.CrossRefGoogle Scholar
da Cruz, L. P., Novaes, D. D. and Torregrosa, J., New lower bound for the Hilbert number in piecewise quadratic differential systems, J. Diff. Eq. 266(7) (2019), 4170–4203.CrossRefGoogle Scholar
Fatou, P., Sur le mouvement d'un système soumis à des forces à courte période, Bull. Soc. Math. France 56 (1928), 98–139.CrossRefGoogle Scholar
Filippov, A. F., Differential equations with discontinuous righthand sides, Mathematics and its Applications (Soviet Series), Volume 18 (Kluwer Academic Publishers Group, Dordrecht, 1988).CrossRefGoogle Scholar
Freire, E., Ponce, E. and Torres, F., Canonical discontinuous planar piecewise linear systems, SIAM J. Appl. Dyn. Syst. 11(1) (2012), 181–211.CrossRefGoogle Scholar
Freire, E., Ponce, E. and Torres, F., The discontinuous matching of two planar linear foci can have three nested crossing limit cycles, Publ. Mat. 58(suppl.) (2014), 221–253.CrossRefGoogle Scholar
Freire, E., Ponce, E., Torregrosa, J. and Torres, F., Limit cycles from a monodromic infinity in planar piecewise linear systems, J. Math. Anal. Appl. 496(2) (2021), 124818.CrossRefGoogle Scholar
Giannakopoulos, F. and Pliete, K., Planar systems of piecewise linear differential equations with a line of discontinuity, Nonlinearity 14(6) (2001), 1611–1632.CrossRefGoogle Scholar
Giné, J., Higher order limit cycle bifurcations from non-degenerate centers, Appl. Math. Comput. 218(17) (2012), 8853–8860.Google Scholar
Giné, J., Limit cycle bifurcations from a non-degenerate center, Appl. Math. Comput. 218(9) (2012), 4703–4709.Google Scholar
Giné, J., Gouveia, L. F. S. and Torregrosa, J., Lower bounds for the local cyclicity for families of centers, J. Diff. Eq. 275 (2021), 309–331.CrossRefGoogle Scholar
Gouveia, L. F. S. and Torregrosa, J., 24 crossing limit cycles in only one nest for piecewise cubic systems, Appl. Math. Lett. 103 (2020), 106189.CrossRefGoogle Scholar
Gouveia, L. F. S. and Torregrosa, J., Local cyclicity in low degree planar piecewise polynomial vector fields, Nonlinear Anal. Real World Appl. 60 (2021), 103278.CrossRefGoogle Scholar
Gouveia, L. F. S. and Torregrosa, J., Lower bounds for the local cyclicity of centers using high order developments and parallelization, J. Diff. Eq. 271 (2021), 447–479.CrossRefGoogle Scholar
Han, M., Bifurcation theory of limit cycles (Science Press Beijing, Alpha Science International Ltd, Beijing, Oxford, 2017).Google Scholar
Han, M. and Yang, J., The maximum number of zeros of functions with parameters and application to differential equations, J. Nonlinear Model. Anal. 3(1) (2021), 13–34.Google Scholar
Han, M. and Yu, P., Normal forms, Melnikov functions and bifurcations of limit cycles, Applied Mathematical Sciences, Volume 181 (Springer, London, 2012).CrossRefGoogle Scholar
Han, M. and Zhang, W., On Hopf bifurcation in non-smooth planar systems, J. Diff. Equ. 248(9) (2010), 2399–2416.CrossRefGoogle Scholar
Han, M., Romanovski, V. G. and Zhang, X., Equivalence of the Melnikov function method and the averaging method, Qual. Theory Dyn. Syst. 15(2) (2016), 471–479.CrossRefGoogle Scholar
Han, M., Sheng, L. and Zhang, X., Bifurcation theory for finitely smooth planar autonomous differential systems, J. Differ. Eq. 264 (2018), 3596–3618.CrossRefGoogle Scholar
Huan, S.-M. and Yang, X.-S., On the number of limit cycles in general planar piecewise linear systems, Discrete Contin. Dyn. Syst. 32(6) (2012), 2147–2164.CrossRefGoogle Scholar
Ilyashenko, Y., Centennial history of Hilbert's 16th problem, Bull. Amer. Math. Soc. (N.S.) 39(3) (2002), 301–354.CrossRefGoogle Scholar
Itikawa, J., Llibre, J. and Oliveira, R., Private Communication.Google Scholar
Kuznetsov, Y. A., Elements of applied bifurcation theory, Applied Mathematical Sciences, Volume 112, 3rd edn. (Springer-Verlag, New York, 2004).CrossRefGoogle Scholar
Leine, R. I. and van Campen, D. H., Discontinuous bifurcations of periodic solutions, Math. Comput. Model. 36(3) (2002), 259–273. Mathematical modelling of nonlinear systems (Leeds, 1999).CrossRefGoogle Scholar
Liang, H. and Torregrosa, J., Parallelization of the Lyapunov constants and cyclicity for centers of planar polynomial vector fields, J. Diff. Equ. 259(11) (2015), 6494–6509.CrossRefGoogle Scholar
Llibre, J. and Ponce, E., Three nested limit cycles in discontinuous piecewise linear differential systems with two zones, Dyn. Contin. Discrete Impuls. Syst. Ser. B Appl. Algorithms 19(3) (2012), 325–335.Google Scholar
Llibre, J. and Tang, Y., Limit cycles of discontinuous piecewise quadratic and cubic polynomial perturbations of a linear center, Discrete Contin. Dyn. Syst. Ser. B 24(4) (2019), 1769–1784.Google Scholar
Llibre, J., Novaes, D. D. and Teixeira, M. A., Corrigendum: Higher order averaging theory for finding periodic solutions via Brouwer degree (2014 Nonlinearity 27, 563), Nonlinearity 27(9) (2014), 2417.CrossRefGoogle Scholar
Llibre, J., Novaes, D. D. and Teixeira, M. A., Higher order averaging theory for finding periodic solutions via Brouwer degree, Nonlinearity 27(3) (2014), 563–583.CrossRefGoogle Scholar
Llibre, J., Mereu, A. C. and Novaes, D. D., Averaging theory for discontinuous piecewise differential systems, J. Diff. Equ. 258(11) (2015), 4007–4032.CrossRefGoogle Scholar
Perko, L., Differential equations and dynamical systems, Texts in Applied Mathematics, Volume 7, 3rd edn. (Springer-Verlag, New York, 2001).CrossRefGoogle Scholar
Roussarie, R., Bifurcation of planar vector fields and Hilbert's sixteenth problem, Progress in Mathematics, Volume 164 (Birkhäuser Verlag, Basel, 1998).CrossRefGoogle Scholar
Sanders, J. A. and Verhulst, F., Averaging methods in nonlinear dynamical systems, Applied Mathematical Sciences, Volume 59. (Springer-Verlag, New York, 1985).CrossRefGoogle Scholar
Sibirskiĭ, K. S., On the number of limit cycles in the neighborhood of a singular point, Differencial'nye Uravnenija 1 (1965), 53–66.Google Scholar
Verhulst, F., Nonlinear differential equations and dynamical systems, 2nd ed., Universitext (Springer-Verlag, Berlin, 1996).CrossRefGoogle Scholar
Yu, P. and Tian, Y., Twelve limit cycles around a singular point in a planar cubic-degree polynomial system, Commun. Nonlinear Sci. Numer. Simul. 19(8) (2014), 2690–2705.CrossRefGoogle Scholar
Żoła̧dek, H., On certain generalization of the Bautin's theorem, Nonlinearity 7(1) (1994), 233–279.CrossRefGoogle Scholar
Żoła̧dek, H., Eleven small limit cycles in a cubic vector field, Nonlinearity 8(5) (1995), 843–860.CrossRefGoogle Scholar
Żoła̧dek, H., Remarks on: The classification of reversible cubic systems with center, Topol. Methods Nonlinear Anal. 8(2) (1996), 335–342. [Topol. Methods Nonlinear Anal. 4 (1994), no. 1, 79–136].CrossRefGoogle Scholar
Żoła̧dek, H., The CD45 case revisited. In Mathematical Sciences with Multidisciplinary Applications, pp. 595–625 (Springer International Publishing, Cham, 2016).CrossRefGoogle Scholar