Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T18:58:01.528Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear diophantine equations with cyclic coefficient matrices and its applications to Riemann surfaces

Published online by Cambridge University Press:  20 January 2009

Nobumasa Takigawa
Nobumasa Takigawa
Affiliation:
Department of Applied Mathematics, Okayama University of Science, Ridai-cho, Okayama, 700, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let co, c1, …, cn-1 be the nonzero complex numbers and let C = (cu+1,v+1) = (cn+u-v), O≦u,v≦n — 1, be a cyclic matrix, where n + u — v is taken modulo n. In this paper we shall give the solution of the linear equations

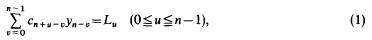
where Lu (0≦u≦n —1) is a fixed complex number. In Theorem 1 weshall give a necessary and sufficient condition for (1) to have an integral solution.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 3 , October 1985 , pp. 369 - 380
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Carlitz, L. and Olson, F. R., Maillet's determinant, Proc. Amer. Math. Soc. (1955), 265–269.Google Scholar
2.Carlitz, L., A generalization of Maillet's determinant and a bound for the first factor of the class number, Proc. Amer. Math. Soc. 12 (1961), 256–261.Google Scholar
3.Harvey, W. J., Cyclic groups of automorphisms of a compact Riemann surface, Quart, J. Math. Oxford 17 (1966), 86–97.CrossRefGoogle Scholar
4.Harvey, W. J., On branch loci in Teichmuller space, Trans. Amer. Math. Soc. 153 (1971), 387–399.Google Scholar
5.Kato, T., Non-hyperelliptic Weierstrass points of maximal weight, Math. Ann. 239 (1979, 141–147.CrossRefGoogle Scholar
6.Lewittes, J., Automorphisms of compact Riemann surfaces, Amer. J. Math. 84 (1963), 734–752.CrossRefGoogle Scholar
7.Lloyd, E. K., Some combinatorial problems in the theory of Riemann surface transformation groups (Ph.D. Thesis, Birmingham, 1967).Google Scholar
8.Macbeath, A. M., On a curve of genus 7, Proc. London Math. Soc. 15 (1965), 527–542.CrossRefGoogle Scholar
9.Maclachlan, C., Weierstrass points on compact Riemann surfaces, J. London Math. Soc. 3 (1971), 722–724.CrossRefGoogle Scholar
10.Metsãnkylã, T., üiber den ersten Faktor der Klassenzahl des Kreiskõrpers, Ann, Acad. Sci. Fenn. AI 416, (1967).Google Scholar
11.Ore, O., Some studies on cyclic determinants, Duke Math. J. 18 (1951), 343–354.CrossRefGoogle Scholar
12.Takioawa, N., Weierstrass points on compact Riemann surfaces with nontrivial automorphisms, J. Math. Soc. Japan 33 (1981), 235–246.Google Scholar
13.Washington, L. C., Cyclotomic fields (Springer verlag, 1982).CrossRefGoogle Scholar