Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-02T22:32:42.968Z Has data issue: false hasContentIssue false
  • English
  • Français

L-ideals of M(G) determined by continuity of translation

Published online by Cambridge University Press:  20 January 2009

Gavin Brown  and
William Moran
Gavin Brown
Affiliation:
Department of Pure Mathematics, University of Liverpool
William Moran
Affiliation:
Department of Pure Mathematics, University of Liverpool
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

G denotes a locally compact abelian group and M(G) the convolution algebra of regular bounded Borel measures on G. An ideal I of M(G) closed in the usual (total variation) norm topology is called an L-ideal if μ ∈ I, ν≪ μ (ν absolutely continuous with respect to μ) implies that ν ∈ I. Here we are concerned with the L-idealsL1(G), 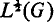, and M0(G) where, as usual, L1(G) denotes the set of measures absolutely continuous with respect to Haar measure, 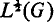denotes the radical of L1(G) in M(G) and M0(G) denotes the set of measures whose Fourier-Stieltjes transforms vanish at infinity.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 18 , Issue 4 , December 1973 , pp. 307 - 316
Copyright
Copyright © Edinburgh Mathematical Society 1973

References

REFERENCES

(1) Brown, G. and Moran, W., On the Silov boundary of a measure algebra, Bull. London Math. Soc. 3 (1971), 197–203.Google Scholar
(2) Glicksberg, I., Uniform boundedness on groups, Canad. J. Math. 14 (1962), 269–276.Google Scholar
(3) Goldberg, R. R. and Simon, A. B., Characterization of some classes of measures, Acta Sci. Math. (Szeged) 17 (1966), 157–161.Google Scholar
(4) Halmos, P. R., Measure Theory (Princeton, 1950).Google Scholar
(5) Taylor, J. L., Convolution measure algebras with group maximal ideal spaces, Trans. Amer. Math. Soc. 128 (1967), 257–263.Google Scholar