Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T03:14:15.304Z Has data issue: false hasContentIssue false
  • English
  • Français

The length of the continued fraction expansion for a class of rational functions in

Published online by Cambridge University Press:  20 January 2009

Arnold Knopfmacher
Arnold Knopfmacher
Affiliation:
Department of Computational and Applied MathematicsUniversity of the WitwatersrandJohannesburg, P O Wits 2050, South Africa
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

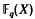
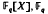A study is made of the length L(h, k) of the continued fraction algorithm for h/k where h and k are co-prime polynomials in a finite field. In addition we investigate the sum of the degrees of the partial quotients in this expansion for 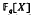h/k, h, k in . The above continued fraction is determined by means of the Euclidean algorithm for the polynomials h, k in .

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 34 , Issue 1 , February 1991 , pp. 7 - 17
Copyright
Copyright © Edinburgh Mathematical Society 1991

References

REFERENCES

1.Dixon, J. D., The numbers of steps in the Euclidean algorithm, J. Number Theory 2 (1970), 414–422.CrossRefGoogle Scholar
2.Heilbronn, H., On the average length of a class of finite continued fractions, in Number Theory and Analysis (Plenum Press, New York, 1969), 87–96.CrossRefGoogle Scholar
3.Killian, H., Zur mittleren Anzahl von Schritten beim eukklidischen Algorithmus, Elem. Math. 38 (1983), 11–15.Google Scholar
4.Knopfmacher, A. and Knopfmacher, J., The exact length of the Euclidean algorithm in , Mathematika 35 (1988), 297–304.CrossRefGoogle Scholar
5.Panov, A. A., Averages over elements of a certain class of finite continued fractions, Russian Math. Surveys 35 (1980), 182–183.CrossRefGoogle Scholar
6.porter, J. W., On a theorem of Heilbronn, Mathematika 22 (1975), 20–28.CrossRefGoogle Scholar
7.Riordan, J., An Introduction to Combinatorial Analysis (Princeton University Press, Princeton, N.J., 1978).Google Scholar