Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2025-01-04T21:50:38.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Lacunary Müntz systems

Published online by Cambridge University Press:  20 January 2009

Peter Borwein  and
Tamás Erdélyi
Peter Borwein
Affiliation:
Department of Mathematics, Dalhousie University, Halifax, Nova Scotia, Canada, B3H 3J5
Tamás Erdélyi
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, Ohio 43210, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical theorem of Müntz and Szász says that the span of

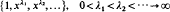
is dense in C[0,1] in the uniform norm if and only if 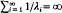. We prove that, if {λi} is lacunary, we can replace the underlying interval [0,1] by any set of positive measure. The key to the proof is the establishment of a bounded Remez-type inequality for lacunary Müntz systems. Namely if A ⊆ [0,1] and its Lebesgue measure µ(A) is at least ε > 0 then

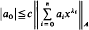
where c depends only on ε and Λ (not on n and A) and where Λ:=infiλi+1/λi>1.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 36 , Issue 3 , October 1993 , pp. 361 - 374
Copyright
Copyright © Edinburgh Mathematical Society 1993

References

REFERENCES

1.Borwein, P. B., Zeros of Chebyshev polynomials in Markov systems, J. Approx. Theory 63 (1990), 56–64.CrossRefGoogle Scholar
2.Borwein, P. B. and Saff, E., On the denseness of weighted incomplete approximations, in Gonchar, A. A. and Saff, E. B. (Eds.), Progress in Approximation Theory (Springer-Verlag, 1992), 419–429.CrossRefGoogle Scholar
3.Borwein, P. B., Variations on Müntz's theme, Canad. Math. Bull. 34 (1991), 305–310.CrossRefGoogle Scholar
4.Cheney, E. W., Introduction to Approximation Theory (McGraw-Hill, New York, 1966).Google Scholar
5.Clarkson, J. A. and Erdös, P., Approximation by polynomials, Duke Math J. 10 (1943), 5–11.CrossRefGoogle Scholar
6.Erdélyi, T., Remez-type inequalities on the size of generalized polynomials, J. London Math. Soc. 45 (1992), 255–264.CrossRefGoogle Scholar
7.Feinerman, R. P. and Newman, D. J., Polynomial Approximation (Williams and Wilkins, Baltimore, MD, 1976).Google Scholar
8.Von Golitschek, M., A short proof of Müntz's theorem, J. Approx. Theory 39 (1983), 394–395.CrossRefGoogle Scholar
9.Hirschman, I. I. Jr., Approximation by non-dense sets of functions, Ann. of Math. 50 (1949), 666–675.CrossRefGoogle Scholar
10.Leviatan, D., Improved estimates in Müntz-Jackson theorems, manuscript.Google Scholar
11.McCarthy, P. C., Sayre, J. E. and Shawyer, B. L. R., Generalized Legendre polynomials, manuscript.Google Scholar
12.Newman, D. J., Derivative bounds for Müntz polynomials, J. Approx. Theory 18 (1976), 360–362.CrossRefGoogle Scholar
13.Newman, D. J., Approximation with rational functions, Regional Conference Series in Mathematics 41 (1978).Google Scholar
14.Schwartz, L., Etude des Sommes d'Exponentielles (Hermann, Paris, 1959).Google Scholar
15.Smith, P. W., An improvement theorem for Descartes systems, Proc. Amer. Math. Soc. 70 (1978), 26–30.CrossRefGoogle Scholar
16.Trent, T. T., A Müntz-Szász theorem for C(D), Proc. Amer. Math. Soc. 83 (1981), 296–298.Google Scholar