Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T03:34:28.812Z Has data issue: false hasContentIssue false
  • English
  • Français

KSBA compactification of the moduli space of K3 surfaces with a purely non-symplectic automorphism of order four

Part of: Families, fibrations Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  12 April 2021

Han-Bom Moon  and
Luca Schaffler
Han-Bom Moon
Affiliation:
Department of Mathematics, Fordham University, New York, NY10023, USA ([email protected])
Luca Schaffler
Affiliation:
Department of Mathematics, KTH Royal Institute of Technology, SE-100 44Stockholm, Sweden ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe a compactification by KSBA stable pairs of the five-dimensional moduli space of K3 surfaces with a purely non-symplectic automorphism of order four and $U(2)\oplus D_4^{\oplus 2}$ lattice polarization. These K3 surfaces can be realized as the minimal resolution of the double cover of $\mathbb {P}^{1}\times \mathbb {P}^{1}$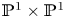 branched along a specific $(4,\,4)$ 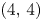curve. We show that, up to a finite group action, this stable pairs compactification is isomorphic to Kirwan's partial desingularization of the GIT quotient $(\mathbb {P}^{1})^{8}{/\!/}\mathrm {SL}_2$ 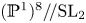with the symmetric linearization.

Keywords

K3 surfacestable pairmoduli spacecompactification

MSC classification

Primary: 14J10: Families, moduli, classification
Secondary: 14J28: $K3$ surfaces and Enriques surfaces 14D06: Fibrations, degenerations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 1 , February 2021 , pp. 99 - 127
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexeev, V., Moduli spaces $M_{g,n}(W)$ for surfaces, pp. 1–22, Higher-Dimensional Complex Varieties (Trento, 1994) (de Gruyter, Berlin, 1996).Google Scholar
Alexeev, V., Moduli of weighted hyperplane arrangements (eds. G. Bini, M. Lahoz, E. Macrì, and P. Stellari), Advanced Courses in Mathematics (CRM Barcelona, Birkhäuser/Springer, Basel, 2015).Google Scholar
Alexeev, V. and Pardini, R., Explicit compactifications of moduli spaces of Campedelli and Burniat surfaces, (2009) arXiv:0901.4431.Google Scholar
Alexeev, V. and Pardini, R., Non-normal abelian covers, Compos. Math. 148 (2012), 1051–1084.CrossRefGoogle Scholar
Alexeev, V. and Thompson, A., ADE surfaces and their moduli, J. Algebraic Geom., Published electronically: November 19, 2020, https://doi.org/10.1090/jag/762.CrossRefGoogle Scholar
Alexeev, V., Engel, P. and Thompson, A., Stable pair compactification of moduli of K3 surfaces of degree 2, (2019) arXiv:1903.09742.Google Scholar
Artebani, M. and Sarti, A., Symmetries of order four on K3 surfaces, J. Math. Soc. Japan 67 (2015), 503–533.CrossRefGoogle Scholar
Ascher, K. and Bejleri, D., Compact moduli of elliptic K3 surfaces, (2019) arXiv:1902.10686.Google Scholar
Barth, W., Hulek, K., Peters, C. and Van de Ven, A., Compact complex surfaces, 2nd edn., pp. xii+436, Ergebnisse der Mathematik und ihrer Grenzgebiete, Volume 3 (Folge, Springer-Verlag, Berlin, 2004).CrossRefGoogle Scholar
Deligne, P. and Mostow, G. D., Monodromy of hypergeometric functions and nonlattice integral monodromy, Inst. Hautes Études Sci. Publ. Math. 63 (1986), 5–89.CrossRefGoogle Scholar
Deopurkar, A. and Han, C., Stable log surfaces, admissible covers, and canonical curves of genus $4$, Trans. Am. Math. Soc. 374 (2021), 589–641.CrossRefGoogle Scholar
Dolgachev, I. and Kondō, S., Moduli of K3 surfaces and complex ball quotients, in Arithmetic and geometry around hypergeometric functions, pp. 43–100, Progr. Math., Volume 260 (Birkhäuser, Basel, 2007).CrossRefGoogle Scholar
Fujino, O., Fundamental theorems for semi log canonical pairs, Algebr. Geom. 1 (2014), 194–228.CrossRefGoogle Scholar
Gallardo, P., Kerr, M. and Schaffler, L., Geometric interpretation of toroidal compactifications of moduli of points in the line and cubic surfaces, to appear in Advances in Mathematics, 381 (2021), https://doi.org/10.1016/j.aim.2021.107632.CrossRefGoogle Scholar
Gallardo, P., Martinez-Garcia, J. and Zhang, Z., Compactifications of the moduli space of plane quartics and two lines, Eur. J. Math. 4 (2018), 1000–1034.Google Scholar
Hacking, P., Keel, S. and Tevelev, J., Stable pair, tropical, and log canonical compactifications of moduli spaces of del Pezzo surfaces, Invent. Math. 178 (2009), 173–227.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, pp. xvi+496, Graduate Texts in Mathematics, Volume 52 (Springer-Verlag, New York-Heidelberg, 1977).CrossRefGoogle Scholar
Hassett, B., Moduli spaces of weighted pointed stable curves, Adv. Math. 173 (2003), 316–352.CrossRefGoogle Scholar
Ishii, S., Introduction to singularities, 2nd edn., pp. x+236 (Springer, Tokyo, 2018).Google Scholar
Kiem, Y.-H. and Moon, H.-B., Moduli spaces of weighted pointed stable rational curves via GIT, Osaka J. Math. 48 (2011), 1115–1140.Google Scholar
Kirwan, F., Partial desingularisations of quotients of nonsingular varieties and their Betti numbers, Ann. Math. (2) 122 (1985), 41–85.Google Scholar
Kollár, J., Singularities of the minimal model program, With a collaboration of Sándor Kovács. Cambridge Tracts in Mathematics, Volume 200 (Cambridge University Press, Cambridge, 2013).Google Scholar
Kollár, J., Families of varieties of general type (Book in preparation, 2018).Google Scholar
Kollár, J. and Shepherd-Barron, N., Threefolds and deformations of surface singularities, Invent. Math. 91 (1988), 299–338.CrossRefGoogle Scholar
Kondō, S., The moduli space of 8 points on $\mathbb {P}^{1}$ and automorphic forms, Algebraic geometry, pp. 89–106, Contemporary Mathematics, Volume 422 (American Mathematical Society, Providence, RI, 2007).Google Scholar
Kulikov, V. S., Degenerations of K3 surfaces and Enriques surfaces, Math. USSR Izv. 11 (1977), 957–989.CrossRefGoogle Scholar
Laza, R. and O'Grady, K., GIT versus Baily--Borel compactification for K3's which are double covers of $\mathbb{P}^1\times\mathbb{P}^1$ (2018) arXiv:1801.04845.Google Scholar
Lazarsfeld, R., Positivity in algebraic geometry. I. Classical setting: line bundles and linear series, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], Volume 48 (Springer-Verlag, Berlin, 2004).Google Scholar
Looijenga, E., New compactifications of locally symmetric varieties, Proceedings of the 1984 Vancouver conference in algebraic geometry, pp. 341–364, CMS Conf. Proc., Volume 6 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Mnëv, N., Varieties of combinatorial types of projective configurations and convex polyhedra, Dokl. Akad. Nauk SSSR 283 (1985), 1312–1314.Google Scholar
Mumford, D., Fogarty, J. and Kirwan, F., Geometric invariant theory, 3rd edn., pp. xiv+292, Ergebnisse der Mathematik und ihrer Grenzgebiete (2), Volume 34 (Springer-Verlag, Berlin, 1994).Google Scholar
Olsson, M., Algebraic spaces and stacks, pp. xi+298, American Mathematical Society Colloquium Publications, Volume 62 (American Mathematical Society, Providence, RI, 2016).Google Scholar
Persson, U. and Pinkham, H., Degeneration of surfaces with trivial canonical bundle, Ann. Math. (2) 113 (1981), 45–66.CrossRefGoogle Scholar
Schaffler, L., The KSBA compactification of the moduli space of $D_{1,6}$-polarized Enriques surfaces, (2016) arXiv:1608.02564.Google Scholar
Shah, J., Degenerations of K3 surfaces of degree $4$, Trans. Am. Math. Soc. 263 (1981), 271–308.Google Scholar
Vakil, R., Murphy's law in algebraic geometry: badly-behaved deformation spaces, Invent. Math. 164 (2006), 569–590.CrossRefGoogle Scholar
Zhang, D.-Q., Automorphisms of K3 surfaces, Proceedings of the International Conference on Complex Geometry and Related Fields, pp. 379–392, AMS/IP Stud. Adv. Math., Volume 39 (American Mathematical Society, Providence, RI, 2007).Google Scholar