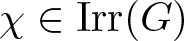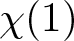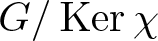Kernels of minimal characters of solvable groups

Abstract

Let G be a finite solvable group. We prove that if $\chi\in{{\operatorname{Irr}}}(G)$ has odd degree and $\chi(1)$ is the minimal degree of the nonlinear irreducible characters of G, then $G/\operatorname{Ker}\chi$ is nilpotent-by-abelian.

1. Introduction

A classical theorem of Broline and Garrison implies that if an irreducible character χ of a finite group G has maximal degree then $\operatorname{Ker}\chi$ is nilpotent (Corollary 12.20 of [1]). This result was extended by Isaacs, who considered characters of nth maximal degree in [2], and proved that if $\chi\in{{\operatorname{Irr}}}(G)$ has nth maximal degree, then the Fitting height of the solvable radical of $\operatorname{Ker}\chi$ is at most n.

Our goal in this note is to consider irreducible characters at the other extreme. Of course, if $\chi\in{{\operatorname{Irr}}}(G)$ is linear, then $G'\leq\operatorname{Ker}\chi$ and $G/\operatorname{Ker}\chi$ is abelian. But can we restrict the structure of $G/\operatorname{Ker}\chi$ if $\chi(1)$ is “small”? This is the content of our main result. We write $m(G)=\min\{\chi(1)\mid\chi\in{{\operatorname{Irr}}}(G), \chi(1) \gt 1\}$. We say that $\chi\in{{\operatorname{Irr}}}(G)$ is a minimal character if $\chi(1)=m(G)$.

Theorem A. Let G be a solvable finite group. Suppose that m(G) is odd. If $\chi\in{{\operatorname{Irr}}}(G)$ is a minimal character, then $G/\operatorname{Ker}\chi$ is nilpotent-by-abelian.

As $\operatorname{GL}_2(3)$ shows, some hypothesis on m(G) is definitely necessary. The Frobenius group of order 20 acting faithfully on an extraspecial 2-group of order 2⁵ is an example with faithful minimal characters of degree 4. We do not know whether it is enough to assume that m(G) is not a power of 2. On the other hand, some solvability hypothesis is definitely necessary: consider any non-abelian simple group with odd degree minimal characters (for instance, $\mathsf{A}_5$). Theorem A follows from applying the next result to $G/\operatorname{Ker}\chi$.

Theorem B. Let G be a finite solvable group. Suppose that $\chi\in{{\operatorname{Irr}}}(G)$ is a faithful minimal character. If $\chi(1)$ is odd, then G is nilpotent-by-abelian.

Note that the structure of groups with all minimal characters faithful was described in detail by Robinson in [6, 7]. In particular, as shown in Lemma 2.1 of [6], solvable groups with all minimal characters faithful are nilpotent-by-abelian. The examples mentioned above show that this is not the case if we just assume that G has a minimal faithful character. Our proof of Theorem B relies on some of the ideas developed by Robinson.

2. Proofs

We argue as in Lemma 2 of [7] to prove our first lemma.

Lemma 2.1. Let G be a finite group. Suppose that $\chi\in{{\operatorname{Irr}}}(G)$ is a primitive faithful minimal character of G. If $N\trianglelefteq G$ is non-central, then $\chi_N\in{{\operatorname{Irr}}}(N)$.

Proof. Suppose that $\chi_N\not\in{{\operatorname{Irr}}}(N)$. Then there exists a central extension $G^*$ of G and $\alpha,\beta\in{{\operatorname{Irr}}}(G^*)$ such that $\chi=\alpha\beta$, where $\alpha,\beta$ are primitive nonlinear irreducible characters of $G^*$. Without loss of generality, we may assume that $\alpha(1)\leq\chi(1)^{1/2}$. Since $1_{G^*}$ is an irreducible constituent of $\alpha\overline{\alpha}$, the minimality of $\chi(1)$ implies that $\alpha\overline{\alpha}$ is a sum of linear characters. Hence $(G^*)'\leq\operatorname{Ker}(\alpha\overline{\alpha})$. In particular, $(G^*)'\leq{\mathbf{Z}}(\alpha)$. By Lemma 2.27 of [1], ${\mathbf{Z}}(\alpha)/\operatorname{Ker}\alpha\leq{\mathbf{Z}}(G^*/\operatorname{Ker}\alpha)$. If follows that $G^*/\operatorname{Ker}\alpha$ is nilpotent (of class at most 2). But α is nonlinear and primitive. This contradicts Theorem 6.22 of [1].

Next, we handle the primitive case of Theorem B. We refer the reader to [3] for the definition and basic properties of Gajendragadkar’s p-special characters.

Lemma 2.2. Let G be a solvable group. Suppose that $\chi\in{{\operatorname{Irr}}}(G)$ is a primitive faithful minimal character. Then $\chi(1)$ is a power of a prime p. Furthermore, if p > 2, then G is nilpotent-by-abelian.

Proof. We may assume that $\chi(1) \gt 1$. By Theorem 2.17 of [3], χ factors as a product of p-special characters, where p runs over the set of prime divisors of $\chi(1)$. Since $\chi(1)=m(G)$, it follows that $\chi(1)=p^n$ is a power of a prime p. This proves the first part of the lemma.

Suppose now that p > 2. Let q ≠ p be a prime. Then $\chi_{\mathbf{O}_q(G)}$ is not irreducible. It follows from Lemma 2.1 that $\mathbf{O}_q(G)$ is central in G. Hence ${\mathbf{F}}(G)=E{\mathbf{Z}}(G)$, where $E=\mathbf{O}_p(G)$. Furthermore, using again Lemma 2.1, every normal abelian subgroup of G is central. Since G has a faithful irreducible character, Theorem 2.32 of [1] implies that ${\mathbf{Z}}(G)$ is cyclic. Now, Corollary 1.10 of [5] implies that E is extraspecial of exponent p. Since $\chi_E\in{{\operatorname{Irr}}}(E)$, we necessarily have that $|E|=p^{2n+1}$.

Note that ${\mathbf{C}}_G(E)={\mathbf{C}}_G({\mathbf{F}}(G))={\mathbf{Z}}(G)$, so $G/{\mathbf{Z}}(G)$ is isomorphic to a subgroup of ${{\operatorname{Aut}}}_{{\mathbf{Z}}(E)}(E)$. By [8], using again that p > 2, we deduce that $G/{\mathbf{F}}(G)$ is isomorphic to a subgroup of $\operatorname{Sp}(2n,p)$. By [4], $\operatorname{Sp}(2n,p)$ has a faithful irreducible representation of dimension $(p^n-1)/2$. Hence $G/{\mathbf{F}}(G)$ has a faithful character of degree $\leq (p^n-1)/2$. Since $m(G)=p^n$, we conclude that $G/{\mathbf{F}}(G)$ has a faithful character that is a sum of linear characters. We conclude that $G/{\mathbf{F}}(G)$ is abelian, as we wanted to prove.

Now, we complete the proof of a slightly strengthened version of Theorem B.

Theorem 2.3. Let G be a solvable group. Suppose that $\chi\in{{\operatorname{Irr}}}(G)$ is a faithful minimal character. If χ is induced from an odd degree character, then G is nilpotent-by-abelian.

Proof. Let $H\leq G$ and $\beta\in{{\operatorname{Irr}}}(H)$ primitive such that $\beta^G=\chi$. Suppose first that $\beta(1)=1$, so that $\chi(1)=|G:H|$. Since 1_G is an irreducible constituent of $(1_H)^G$ and $m(G)=|G:H|=(1_H)^G(1)$, we deduce that $(1_H)^G$ is a sum of linear characters. Hence $G'\leq\operatorname{Ker}(1_H)^G\leq H$. Thus $H\trianglelefteq G$ and by Clifford’s theorem (Theorem 6.2 of [1]), χ_H is a sum of conjugates of β. In particular, χ_H is a sum of linear characters, so $H'\leq\operatorname{Ker}\chi=1$. Hence G is metabelian and the result follows.

Now, we may assume that $\beta(1) \gt 1$ is odd. First, we will see that $H\trianglelefteq G$ and $G'=H'$. Note that $\chi(1)=|G:H|\beta(1) \gt |G:H|$. Hence $(1_H)^G$ is a sum of linear characters and $G'\leq H$, as before. In particular, $H\trianglelefteq G$. Thus H ^ʹ is also normal in G and all the irreducible characters of $G/H'$ have degree divisible by $|G:H| \lt \chi(1)=m(G)$. Hence, ${{\operatorname{Irr}}}(G/H')$ is a set of linear characters, and we conclude that $G'=H'$, as desired.

Now, we claim that $\beta(1)=m(H)$. Let $\mu\in{{\operatorname{Irr}}}(H)$ be nonlinear. Hence, there exists $\nu\in{{\operatorname{Irr}}}(G)$ nonlinear such that $[\mu^G,\nu]\neq 0$. Thus

\begin{equation*} |G:H|\beta(1)=\chi(1)=m(G)\leq\nu(1)\leq\mu^G(1)=|G:H|\mu(1). \end{equation*}

We conclude that $\beta(1)\leq\mu(1)$. The claim follows.

Thus β is a primitive faithful minimal character of $H/\operatorname{Ker}\beta$. By Lemma 2.2, we have that $\beta(1)$ is a power of a prime p. Let $\beta=\beta_1,\dots,\beta_t$ be the G-conjugates of β. Let $K_i=\operatorname{Ker}\beta_i$. Since $\chi=\beta^G$ is faithful, Lemma 5.11 of [1] implies that $\bigcap_{i=1}^tK_i=1$. Since p > 2, by the second part of Lemma 2.2, we have that $H/K_i$ is nilpotent-by-abelian. Write $F_i/K_i={\mathbf{F}}(H/K_i)$, so that $G'=H'\leq F_i$ for every i. By Proposition 9.5 of [5], $\bigcap_{i=1}^tF_i={\mathbf{F}}(H)$. Therefore, $G'\leq {\mathbf{F}}(H)$ and we conclude that G is nilpotent-by-abelian, as wanted.