Article contents
Invariance of KMS states on graph C*-algebras under classical and quantum symmetry
Published online by Cambridge University Press: 20 September 2021
Abstract
We study the invariance of KMS states on graph $C^{\ast }$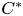 -algebras coming from strongly connected and circulant graphs under the classical and quantum symmetry of the graphs. We show that the unique KMS state for strongly connected graphs is invariant under the quantum automorphism group of the graph. For circulant graphs, it is shown that the action of classical and quantum automorphism groups preserves only one of the KMS states occurring at the critical inverse temperature. We also give an example of a graph $C^{\ast }$
-algebras coming from strongly connected and circulant graphs under the classical and quantum symmetry of the graphs. We show that the unique KMS state for strongly connected graphs is invariant under the quantum automorphism group of the graph. For circulant graphs, it is shown that the action of classical and quantum automorphism groups preserves only one of the KMS states occurring at the critical inverse temperature. We also give an example of a graph $C^{\ast }$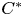 -algebra having more than one KMS state such that all of them are invariant under the action of classical automorphism group of the graph, but there is a unique KMS state which is invariant under the action of quantum automorphism group of the graph.
-algebra having more than one KMS state such that all of them are invariant under the action of classical automorphism group of the graph, but there is a unique KMS state which is invariant under the action of quantum automorphism group of the graph.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 762 - 778
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
- 2
- Cited by



