Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
AZEVEDO, A. C. P.
BASTOS, G. G.
and
JURIAANS, S. O.
2007.
EXTENSION OF AUTOMORPHISMS OF SUBGROUPS OF ABELIAN AND POLYCYCLIC-BY-FINITE GROUPS.
Journal of Algebra and Its Applications,
Vol. 06,
Issue. 02,
p.
315.
Dolinka, Igor
and
Mašulović, Dragan
2011.
Remarks on homomorphism-homogeneous lattices and semilattices.
Monatshefte für Mathematik,
Vol. 164,
Issue. 1,
p.
23.
BASTOS, G. G.
JESPERS, E.
JURIAANS, S. O.
and
E SILVA, A. DE A.
2012.
EXTENSION OF AUTOMORPHISMS OF SUBGROUPS.
Glasgow Mathematical Journal,
Vol. 54,
Issue. 2,
p.
371.


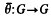 such that
such that 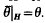 . It is of course well known that the category of groups does not possess non-trivial injective objects and so we consider groups satisfying the weaker condition of quasi-injectivity.
. It is of course well known that the category of groups does not possess non-trivial injective objects and so we consider groups satisfying the weaker condition of quasi-injectivity.