Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jump, K.
1971.
Pseudo-rings of infinite matrices.
Proceedings of the Edinburgh Mathematical Society,
Vol. 17,
Issue. 4,
p.
325.


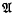 = (
= (