Hostname: page-component-5cf477f64f-54txb Total loading time: 0 Render date: 2025-04-06T15:48:16.732Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher-order evolution inequalities involving convection and Hardy-Leray potential terms in a bounded domain

Part of: Partial differential equations Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  05 May 2023

Huyuan Chen ,
Mohamed Jleli  and
Bessem Samet
Huyuan Chen
Affiliation:
Department of Mathematics, Jiangxi Normal University, Nanchang, Jiangxi 330022, People’s Republic of China ([email protected])
Mohamed Jleli
Affiliation:
Department of Mathematics, College of Science, King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia ([email protected]; [email protected])
Bessem Samet
Affiliation:
Department of Mathematics, College of Science, King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a class of nonlinear higher-order evolution inequalities posed in 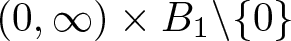$(0,\infty)\times B_1\backslash\{0\}$, subject to inhomogeneous Dirichlet-type boundary conditions, where B1 is the unit ball in 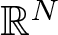$\mathbb{R}^N$. The considered class involves differential operators of the form

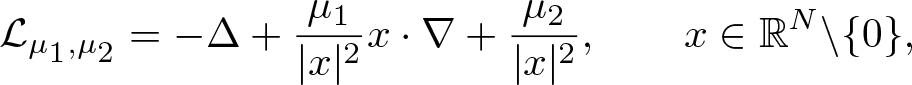\begin{equation*}\mathcal{L}_{\mu_1,\mu_2}=-\Delta +\frac{\mu_1}{|x|^2}x\cdot \nabla +\frac{\mu_2}{|x|^2},\qquad x\in \mathbb{R}^N\backslash\{0\},\end{equation*}
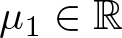where $\mu_1\in \mathbb{R}$ and 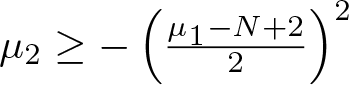$\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$. Optimal criteria for the nonexistence of weak solutions are established. Our study yields naturally optimal nonexistence results for the corresponding class of elliptic inequalities. Notice that no restriction on the sign of solutions is imposed.

Keywords

evolution inequalitiesbounded domaindegenerate operatornonexistencepotential terms

MSC classification

Primary: 35R45: Partial differential inequalities 35B44: Blow-up 35B33: Critical exponents
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 2 , May 2023 , pp. 366 - 390
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdellaoui, B., Peral, I. and Primo, A., Influence of the Hardy potential in a semilinear heat equation, Proc. Roy. Soc. Edinburgh Sect. A 139(5) (2009), 897–926.10.1017/S0308210508000152CrossRefGoogle Scholar
Attar, A., Merchan, S. and Peral, I., A remark on existence of semilinear heat equation involving a Hardy–Leray potential, J. Evol. Equ. 15(1) (2015), 239–250.10.1007/s00028-014-0259-xCrossRefGoogle Scholar
Baras, P. and Goldstein, J., The heat equation with a singular potential, Trans. Amer. Math. Soc. 294 (1984), 121–139.10.1090/S0002-9947-1984-0742415-3CrossRefGoogle Scholar
Cabré, X. and Martel, Y., Existence versus explosion instantanée pour des équations de la chaleur linéaires avec potentiel singulier, C. R. Acad. Sci. Paris Sér. I Math. 329(11) (1999), 973–978.10.1016/S0764-4442(00)88588-2CrossRefGoogle Scholar
Caffarelli, L. A., Kohn, R. and Nirenberg, L., First order interpolation inequalities with weights, Compos. Math. 53 (1984), 259–275.Google Scholar
Chaudhuri, N. and Cirstea, F., On trichotomy of positive singular solutions associated with the Hardy–Sobolev operator, C. R. Math. Acad. Sci. Paris. 347 (2009), 153–158.10.1016/j.crma.2008.12.018CrossRefGoogle Scholar
Chen, H. and Véron, L., Boundary singularities of semilinear elliptic equations with Leray–Hardy potential, Comm. Contemp. Math. 24 (2022), . doi:10.1142/S0219199721500516.CrossRefGoogle Scholar
Chen, H. and Véron, L., Schrödinger operators with Leray–Hardy potential singular on the boundary, J. Differential Equations. 269 (2020), 2091–2131.10.1016/j.jde.2020.01.029CrossRefGoogle Scholar
Chen, H. and Zheng, Y., Qualitative properties for elliptic problems with CKN operators, preprint, arXiv:2206.04247, 2022.Google Scholar
Chen, H., Quaas, A. and Zhou, F., On nonhomogeneous elliptic equations with the Hardy–Leray potentials, J. Anal. Math. 144(1) (2021), 305–334.10.1007/s11854-021-0182-3CrossRefGoogle Scholar
Cirstea, F., A complete classification of the isolated singularities for nonlinear elliptic equations with inverse square potentials, Mem. Amer. Math. Soc. 227(1068) (2014), 1–97.Google Scholar
El Hamidi, A. and Laptev, G. G., Existence and nonexistence results for higher-order semilinear evolution inequalities with critical potential, J. Math. Anal. Appl. 304(2) (2005), 451–463.10.1016/j.jmaa.2004.09.019CrossRefGoogle Scholar
Fabes, E. B., Kenig, C. E. and Serapioni, R. P., The local regularity of solutions of degenerate elliptic equations, Comm. Partial Differential Equations 7(1) (1982), 77–116.10.1080/03605308208820218CrossRefGoogle Scholar
Fall, M. M., Nonexistence of distributional supersolutions of a semilinear elliptic equation with Hardy potential, J. Funct. Anal. 263(8) (2012), 2205–2227.10.1016/j.jfa.2012.06.018CrossRefGoogle Scholar
Filippucci, R., Pucci, P. and Robert, F., On a p-Laplace equation with multiple critical nonlinearities, J. Math. Pures Appl. 91 (2009), 156–177.10.1016/j.matpur.2008.09.008CrossRefGoogle Scholar
Goldstein, G. R., Goldstein, J. A., Kömbe, I. and Tellioglu, R., Nonexistence of positive solutions for nonlinear parabolic Robin problems and Hardy–Leray inequalities, Ann. Math. Pures Appl. 201 (2022), 2927–2942.10.1007/s10231-022-01226-6CrossRefGoogle Scholar
Guerch, B. and Véron, L., Local properties of stationary solutions of some nonlinear singular Schrödinger equations, Rev. Mat. Iberoamericana. 7 (1991), 65–114.10.4171/RMI/106CrossRefGoogle Scholar
Guo, W., Wang, Z. J., Du, R. M. and Wen, L. S., Critical Fujita exponents for a class of nonlinear convection-diffusion equations, Math. Methods Appl. Sci. 34(7) (2011), 839–849.10.1002/mma.1406CrossRefGoogle Scholar
Jleli, M., Samet, B. and Sun, Y., Higher order evolution inequalities with convection terms in an exterior domain of $\mathbb{R}^N$, J. Math. Anal. Appl., 519 (2023), .10.1016/j.jmaa.2022.126738CrossRefGoogle Scholar
Jleli, M., Samet, B. and Vetro, C., On the critical behavior for inhomogeneous wave inequalities with Hardy potential in an exterior domain, Adv. Nonlinear Anal. 10(1) (2021), 1267–1283.10.1515/anona-2020-0181CrossRefGoogle Scholar
Jleli, M., Samet, B. and Ye, D., Critical criteria of Fujita type for a system of inhomogeneous wave inequalities in exterior domains, J. Differential Equations. 268 (2020), 3035–3056.10.1016/j.jde.2019.09.051CrossRefGoogle Scholar
Lei, Y., Qualitative properties of positive solutions of quasilinear equations with Hardy terms, Forum Math. 29 (2017), 1177–1198.10.1515/forum-2014-0173CrossRefGoogle Scholar
Levine, H. A. and Zhang, Q. S., The critical Fujita number for a semilinear heat equation in exterior domains with homogeneous Neumann boundary values, Proc. Roy. Soc. Edinburgh Sect. A 130 (2000), 591–602.10.1017/S0308210500000317CrossRefGoogle Scholar
Li, Y., Nonexistence of p-Laplace equations with multiple critical Sobolev-Hardy terms, Appl. Math. Lett. 60 (2016), 56–60.10.1016/j.aml.2016.04.002CrossRefGoogle Scholar
Merchán, S. and Montoro, L., Remarks on the existence of solutions to some quasilinear elliptic problems involving the Hardy–Leray potential, Ann. Mat. Pures Appl. 193 (2014), 609–632.10.1007/s10231-012-0293-7CrossRefGoogle Scholar
Merchán, S., Montoro, L., Peral, I. and Sciunzi, B., Existence and qualitative properties of solutions to a quasilinear elliptic equation involving the Hardy–Leray potential, Ann. Inst. Henri Poincaré C Anal. Non Linéaire 31(1) (2014), 1–22.Google Scholar
Mitidieri, E. and Pokhozhaev, S. I., A priori estimates and blowup of solutions to nonliner partial differential equations and inequalities, Proc. Steklov Inst. Math. 234 (2001), 1–362.Google Scholar
Montoro, L. and Sciunzi, B., Qualitative properties of solutions to the Dirichlet problem for a Laplace equation involving the Hardy potential with possibly boundary singularity, Math. Eng. 5(1) (2023), 1–16.10.3934/mine.2023017CrossRefGoogle Scholar
Muckenhoupt, B., Weighted norm inequalities for the Hardy maximal function, Trans. Amer. Math. Soc. 165 (1972), 207–226.10.1090/S0002-9947-1972-0293384-6CrossRefGoogle Scholar
Na, Y., Zhou, M., Zhou, X. and Gai, G., Blow-up theorems of Fujita type for a semilinear parabolic equation with a gradient term, Adv. Difference Equations 2018 (2018), .10.1186/s13662-018-1582-2CrossRefGoogle Scholar
Sire, Y., Terracini, S. and Vita, S., Liouville type theorems and regularity of solutions to degenerate or singular problems part I: even solutions, Comm. Partial Differential Equations 46(2) (2021), 310–361.10.1080/03605302.2020.1840586CrossRefGoogle Scholar
Sun, Y., The absence of global positive solutions to semilinear parabolic differential inequalities in exterior domain, Proc. Amer. Math. Soc. 145(8) (2017), 3455–3464.10.1090/proc/13472CrossRefGoogle Scholar
Vazquez, J. L. and Zuazua, E., The Hardy inequality and the asymptotic behaviour of the heat equation with an inverse-square potential, J. Funct. Anal. 173(1) (2000), 103–153.10.1006/jfan.1999.3556CrossRefGoogle Scholar
Wang, L., Wei, Q. and Kang, D., Multiple positive solutions for p-Laplace elliptic equations involving concave-convex nonlinearities and a Hardy-type term, Nonlinear Anal. 74 (2011), 626–638.10.1016/j.na.2010.09.017CrossRefGoogle Scholar
Wang, Z. Q. and Willem, M., Caffarelli-Kohn-Nirenberg inequalities with remainder terms, J. Funct. Anal. 203(2) (2003), 550–568.10.1016/S0022-1236(03)00017-XCrossRefGoogle Scholar
Zhang, Q. S., A general blow-up result on nonlinear boundary-value problems on exterior domains, Proc. Roy. Soc. Edinburgh Sect. A 131(2) (2001), 451–475.10.1017/S0308210500000950CrossRefGoogle Scholar
Zheng, S. and Wang, C., Large time behaviour of solutions to a class of quasilinear parabolic equations with convection terms, Nonlinearity 21 (2008), 2179–2200.10.1088/0951-7715/21/9/015CrossRefGoogle Scholar
Zhou, Q., Nie, Y. and Han, X., Large time behavior of solutions to semilinear parabolic equations with gradient, J. Dyn. Control Syst. 22(1) (2016), 191–205.10.1007/s10883-015-9294-3CrossRefGoogle Scholar