Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-17T22:59:32.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher order log-concavity of the overpartition function and its consequences

Part of: Combinatorics Multiplicative number theory Error analysis and interval analysis

Published online by Cambridge University Press:  03 April 2023

Gargi Mukherjee ,
Helen W. J. Zhang  and
Ying Zhong
Gargi Mukherjee
Affiliation:
Institute for Algebra, Science park 2, Johannes Kepler University, Altenberger Straße 69, Linz A-4040, Austria ([email protected])
Helen W. J. Zhang
Affiliation:
School of Mathematics, Hunan University, Changsha 410082, People’s Republic of China ([email protected]) Hunan Provincial Key Laboratory of Intelligent Information Processing and Applied Mathematics, Changsha 410082, People’s Republic of China ([email protected])
Ying Zhong
Affiliation:
School of Mathematics, Hunan University, Changsha 410082, People’s Republic of China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 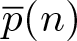${\overline{p}}(n)$ denote the overpartition function. In this paper, we study the asymptotic higher-order log-concavity property of the overpartition function in a similar framework done by Hou and Zhang for the partition function. This will enable us to move on further in order to prove log-concavity of overpartitions, explicitly by studying the asymptotic expansion of the quotient 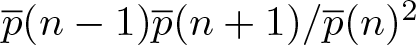${\overline{p}}(n-1){\overline{p}}(n+1)/{\overline{p}}(n)^2$ up to a certain order. This enables us to additionally prove 2-log-concavity and higher Turán inequalities with a unified approach.

Keywords

overpartition functionRademacher-type seriesr-log-concavityhigher order Turán inequalitieslog-concavity

MSC classification

Primary: 05A20: Combinatorial inequalities 11N37: Asymptotic results on arithmetic functions 65G99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 1 , February 2023 , pp. 164 - 181
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, G. E., The theory of partitions (Cambridge University Press, Cambridge, 1998).Google Scholar
Chen, W. Y. C.. Recent developments on log-concavity and q-log-concavity of combinatorial polynomials, in FPSAC 2010 Conference Talk Slides, 2010. http://www.billchen.org/talks/2010-FPSAC.Google Scholar
Chen, W. Y. C., Jia, D. X. Q. and Wang, L. X. W., Higher order Turán inequalities for the partition function, Trans. Amer. Math. Soc. 372(3) (2019), 2143–2165.10.1090/tran/7707CrossRefGoogle Scholar
Chen, W. Y. C., Wang, L. X. W. and Xie, G. Y. B., Finite difference of the logarithm of the partition function, Math. Comp. 85(298) (2016), 825–847.10.1090/mcom/2999CrossRefGoogle Scholar
Corteel, S. and Lovejoy, J., Overpartitions, Trans. Amer. Math. Soc. 356 (2004), 1623–1635.10.1090/S0002-9947-03-03328-2CrossRefGoogle Scholar
DeSalvo, S. and Pak, I., Log-concavity of the partition function, Ramanujan J. 38(1) (2015), 61–73.10.1007/s11139-014-9599-yCrossRefGoogle Scholar
Engel, B., Log-concavity of the overpartition function, Ramanujan J. 43(2) (2017), 229–241.10.1007/s11139-015-9762-0CrossRefGoogle Scholar
Hardy, G. H., Twelve lectures on subjects suggested by his life and work (Cambridge University Press, Cambridge, 1940).Google Scholar
Hardy, G. H. and Ramanujan, S., Asymptotic formulae in combinatory analysis, Proc. Lond. Math. Soc. 17 (1918), 75–175.10.1112/plms/s2-17.1.75CrossRefGoogle Scholar
Hou, Q.-H. and Zhang, Z. R., Asymptotic r-log-convexity and P-recursive sequences, J. Symbolic Comput. 93 (2019), 21–33.10.1016/j.jsc.2018.04.012CrossRefGoogle Scholar
Hou, Q.-H. and Zhang, Z. R., r-log-concavity of partition functions, Ramanujan J. 48 (1) (2019) 117–129.10.1007/s11139-017-9975-5CrossRefGoogle Scholar
Jia, D. X. Q. and Wang, L. X. W., Determinantal inequalities for the partition function, Proc. Roy. Soc. Edinburgh Sect. A 150(3) (2020), 1451–1466.10.1017/prm.2018.144CrossRefGoogle Scholar
Larson, H. and Wagner, I., Hyperbolicity of the partition Jensen polynomials, Res. Number Theory 5(2) (2019), .Google Scholar
Lehmer, D. H., On the series for the partition function, Trans. Amer. Math. Soc. 43 (1938), 271–292.10.1090/S0002-9947-1938-1501943-5CrossRefGoogle Scholar
Lehmer, D. H., On the remainders and convergence of the series for the partition function, Trans. Amer. Math. Soc. 46 (1939), 362–373.10.1090/S0002-9947-1939-0000410-9CrossRefGoogle Scholar
Liu, E. Y. S. and Zhang, H. W. J., Inequalities for the overpartition function, Ramanujan J. 54(3) (2021), 485–509.10.1007/s11139-019-00227-zCrossRefGoogle Scholar
Mukherjee, G., Inequalities for the overpartition function arising from determinants, Preprint arXiv:2201.07840, submitted for publication.Google Scholar
Rademacher, H., On the partition function p(n), Proc. Lond. Math. Soc. 2(1) (1938), 241–254.10.1112/plms/s2-43.4.241CrossRefGoogle Scholar
Sills, A. V., A Rademacher type formula for partitions and overpartitions, Int. J. Math. Math. Sci. 2010 (2010), .10.1155/2010/630458CrossRefGoogle Scholar
Zuckerman, H. S., On the coefficients of certain modular forms belonging to subgroups of the modular group, Trans. Amer. Math. Soc. 45(2) (1939), 298–321.10.1090/S0002-9947-1939-1501993-XCrossRefGoogle Scholar