Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T15:14:21.005Z Has data issue: false hasContentIssue false
  • English
  • Français

The Green Rings of Minimal Hopf Quivers

Part of: Representation theory of rings and algebras Grothendieck groups and $K_0$ Categories with structure

Published online by Cambridge University Press:  11 June 2015

Hua-Lin Huang  and
Yuping Yang
Hua-Lin Huang
Affiliation:
School of Mathematics, Shandong University, Jinan 250100, People's Republic of China ([email protected]; [email protected])
Yuping Yang
Affiliation:
School of Mathematics, Shandong University, Jinan 250100, People's Republic of China ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let be a field and let Q be a minimal Hopf quiver, i.e. a cyclic quiver or the infinite linear quiver, and let repln(Q) denote the category of locally nilpotent finite-dimensional -representations of Q. The category repln(Q) has natural tensor structures induced from graded Hopf structures on the path coalgebra 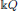. Tensor categories of the form repln(Q) are an interesting class of tame hereditary pointed tensor categories that are not finite. The aim of this paper is to compute the Clebsch–Gordan formulae and Green rings of such tensor categories.

Keywords

Green ringtensor categoryquiver representation

MSC classification

Secondary: 19A22: Frobenius induction, Burnside and representation rings 18D10: Monoidal categories (= multiplicative categories), symmetric monoidal categories, braided categories 16G20: Representations of quivers and partially ordered sets
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 59 , Issue 1 , February 2016 , pp. 107 - 141
Copyright
Copyright © Edinburgh Mathematical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Assem, I., Simson, D. and Skowroński, A., Elements of the representation theory of associative algebras, 1: Techniques of representation theory, London Mathematical Society Student Texts, Volume 65 (Cambridge University Press, 2006).Google Scholar
2. Chen, H., Van Oystaeyen, F. and Zhang, Y., The Green rings of Taft algebras, Proc. Am. Math. Soc. 142 (2014) 765–775.CrossRefGoogle Scholar
3. Cibils, C. and Rosso, M., Hopf quivers, J. Alg. 254(2) (2002), 241–251.Google Scholar
4. Etingof, P., Gelaki, S., Nikshych, D. and Ostrik, V., Tensor categories, Notes from lectures given at the Massachusetts Institute of Technology (2009; available at http://www-math.mit.edu/~etingof/tenscat.pdf).Google Scholar
5. Herschend, M., Tensor products on quiver representations, J. Pure Appl. Alg. 212(2) (2008), 452–469.Google Scholar
6. Herschend, M., On the representation ring of a quiver, Alg. Representat. Theory 12(6) (2009), 513–541.Google Scholar
7. Huang, H.-L., Ye, Y. and Zhao, Q., Hopf structures on the Hopf quiver Q(⟨g⟩, g), Pac. J. Math. 248(2) (2010), 317–334.Google Scholar
8. Huang, H.-L., Van Oystaeyen, F., Yang, Y. and Zhang, Y., The Green rings of pointed tensor categories of finite type, J. Pure Appl. Alg. 218(2) (2014), 333–342.Google Scholar
9. Kinser, R., The rank of a quiver representation, J. Alg. 320(6) (2008), 2363–2387.Google Scholar
10. Kinser, R., Rank functions on rooted tree quivers, Duke Math. J. 152(1) (2010), 27–92.CrossRefGoogle Scholar
11. Li, L. and Zhang, Y., The Green rings of the generalized Taft Hopf algebras, Contemp. Math. 585 (2013), 275–288.Google Scholar
12. Simson, D., Coalgebras of tame comodule type, comodule categories, and a tame–wild dichotomy problem, in Representations of algebras and related topics, pp. 561–660, EMS Series of Congress Reports (European Mathematical Society Publishing House, Zürich, 2011).CrossRefGoogle Scholar