Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-15T08:51:07.067Z Has data issue: false hasContentIssue false
  • English
  • Français

Graph morphisms and exhaustion of curve graphs of low-genus surfaces

Part of: Low-dimensional topology

Published online by Cambridge University Press:  08 April 2025

Jesús Hernández Hernández Open the ORCID record for Jesús Hernández Hernández [Opens in a new window]
Jesús Hernández Hernández*
Affiliation:
Centro de Ciencias Matemáticas, Universidad Nacional Autónoma de México, Morelia, 58089 México
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let S be an orientable, connected surface of finite topological type, with genus 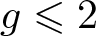$g \leqslant 2$, empty boundary and complexity at least 2; we prove that any graph endomorphism of the curve graph of S is actually an automorphism. Also, as a complement of the author’s previous results, we prove that under mild conditions on the complexity of the underlying surfaces, any graph morphism between curve graphs is induced by a homeomorphism of the surfaces.

To prove these results, we construct a finite subgraph whose union of iterated rigid expansions is the curve graph 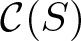$\mathcal{C}(S)$. The sets constructed, and the method of rigid expansion, are closely related to Aramayona and Leininger’s finite rigid sets. We prove as a consequence that Aramayona and Leininger’s rigid set also exhausts 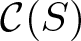$\mathcal{C}(S)$ via rigid expansions. The combinatorial rigidity results follow as an immediate consequence, based on the author’s previous results.

Keywords

curve graphlow-genus surfacerigid expansionsgraph morphisms

MSC classification

Secondary: 57M60: Group actions in low dimensions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 51
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aramayona, J. and Leininger, C. J., Finite rigid sets in curve complexes, J. Topol. Anal. 5(2) (2013), 183–203.CrossRefGoogle Scholar
Aramayona, J. and Leininger, C. J., Exhausting curve complexes by finite rigid sets, Pacific J. Math. 282(2) (2016), 257–283.CrossRefGoogle Scholar
Behrstock, J. and Margalit, D., Curve complexes and finite index subgroups of mapping class groups, Geom. Dedicata 118(1) (2006), 71–85.CrossRefGoogle Scholar
Farb, B. and Margalit, D.. A primer on mapping class groups, Princeton Mathematical Series, volume 49 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Harvey, W. J.. Boundary structure of the modular group, in Riemann surfaces and related topics: Proceedings of the 1978 Stony Brook Conference (State Univ. New York, Stony Brook, N.Y., 1978), Ann. of Math. Stud, volume 97, (Princeton University Press, Princeton, NJ, 1981).CrossRefGoogle Scholar
Hernández Hernández, J., Edge-preserving maps of curve graphs, Topology Appl. 246 (2018), 83–105.CrossRefGoogle Scholar
Hernández Hernández, J., Exhaustion of the curve graph via rigid expansions, Glasg. Math. J. 61(1) (2019), 195–230.CrossRefGoogle Scholar
Irmak, E., Superinjective simplicial maps of complexes of curves and injective homomorphisms of subgroups of mapping class groups, Topology 43(3) (2004), 513–541.CrossRefGoogle Scholar
Irmak, E., Superinjective simplicial maps of complexes of curves and injective homomorphisms of subgroups of mapping class groups. II, Topology Appl. 153(8) (2006), 1309–1340.CrossRefGoogle Scholar
Irmak, E., Complexes of nonseparating curves and mapping class groups, Michigan Math. J. 54(1) (2006), 81–110.CrossRefGoogle Scholar
Irmak, E., Edge preserving maps of the curve graphs in low genus, Topology Proc. 54(1) (2019), 205–231.Google Scholar
Irmak, E., Edge-preserving maps of the nonseparating curve graphs, curve graphs and rectangle preserving maps of the Hatcher-Thurston graphs, J. Knot Theory Ramifications 29(11) (2020), 2050078, 41.CrossRefGoogle Scholar
Shackleton, K. J., Combinatorial rigidity in curve complexes and mapping class groups, Pacific J. Math. 230(1) (2007), 217–232.CrossRefGoogle Scholar
Korkmaz, M., Automorphisms of complexes of curves on punctured spheres and on punctured tori, Topology Appl. 95(2) (1999), 85–111.CrossRefGoogle Scholar
Luo, F., Automorphisms of the complex of curves, Topology 39(2) (2000), 283–298.CrossRefGoogle Scholar
Ivanov, N. V., Automorphism of complexes of curves and of Teichmüller spaces, Internat. Math. Res. Notices 14(14) (1997), 651–666.CrossRefGoogle Scholar