Article contents
The graded Cartan matrix and global dimension of 0-relations algebras
Published online by Cambridge University Press: 20 January 2009
Extract
The Cartan matrix C of a left artinian ring A, with indecomposable projectives P1,…,Pn and corresponding simples Si=Pi/JPi, is an n×n integral matrix with entries Cij, the number of copies of the simple sj which appear as composition factors of Pi. A relationship between the invertibility of this matrix (as an integral matrix) and the finiteness of the global dimension has long been known: gl dim A < ∞⇒det C = ± 1 (Eilenberg [3]). More recently Zacharia [9] has shown that gl dim A ≦ 2⇒det C = 1, and in fact no rings of finite global dimension are known with det C = −1. The converse, det C = l⇒gl dim A < ∞, is false, as easy examples show ([[1) or [3]). However if A is left serial, gl dim A < ∞iff det C = l [1]. If A = ⊕n ≧ 0 An is ℤ-graded and the radical J = ⊕n ≧ 0 An, Wilson [8] calls such rings positively graded. Here there is a graded Cartan matrix 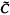 with entries from ℤ[X] and gl dim A < ∞⇒det
with entries from ℤ[X] and gl dim A < ∞⇒det 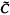 = 1 and, hence, det C = l [8, Prop. 2.2].
= 1 and, hence, det C = l [8, Prop. 2.2].
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 3 , October 1987 , pp. 351 - 362
- Copyright
- Copyright © Edinburgh Mathematical Society 1987
References
REFERENCES
- 5
- Cited by


