Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T21:13:41.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized eigenvalues of the (P, 2)-Laplacian under a parametric boundary condition

Part of: Representations of solutions Elliptic equations and systems Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  18 December 2019

Jamil Abreu  and
Gustavo F. Madeira
Jamil Abreu
Affiliation:
Departamento de Matemática Aplicada, Universidade Federal do Espírito Santo, Rodovia BR101, Km 60, São MateusES, Brazil ([email protected])
Gustavo F. Madeira
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos – UFSCar, Rod. Washington Luís, Km 235 – São CarlosSP, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study a general eigenvalue problem for the so called (p, 2)-Laplace operator on a smooth bounded domain Ω ⊂ ℝN under a nonlinear Steklov type boundary condition, namely

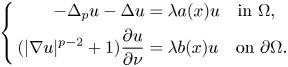\[\left\{ \begin{aligned} -\Delta_pu-\Delta u & =\lambda a(x)u \quad {\rm in}\ \Omega,\\ (|\nabla u|^{p-2}+1)\dfrac{\partial u}{\partial\nu} & =\lambda b(x)u \quad {\rm on}\ \partial\Omega . \end{aligned} \right.\]
For positive weight functions a and b satisfying appropriate integrability and boundedness assumptions, we show that, for all p>1, the eigenvalue set consists of an isolated null eigenvalue plus a continuous family of eigenvalues located away from zero.

Keywords

eigenvalue problemcontinuous family of eigenvalues(p, 2)-LaplacianSteklov boundary conditionboundary condition with eigenvalue parameter

MSC classification

Primary: 35D30: Weak solutions 35J60: Nonlinear elliptic equations
Secondary: 35P30: Nonlinear eigenvalue problems, nonlinear spectral theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 1 , February 2020 , pp. 287 - 303
Copyright
Copyright © Edinburgh Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, R. A. and Fournier, J. J. F., Sobolev spaces, Pure and Applied Mathematics, Volume 140, 2nd edn (Academic Press, 2003). First edition by Adams, R. (Academic Press, 1975).Google Scholar
2Afrouzi, G. and Brown, K., On principal eigenvalues for boundary value problems with indefinite weight and Robin boundary conditions, Proc. Amer. Math. Soc. 127(1) (1999), 125–130.10.1090/S0002-9939-99-04561-XCrossRefGoogle Scholar
3Aizicovici, S., Papageorgiou, N. S. and Staicu, V., Nodal solutions for (p, 2)-equations, Trans. Amer. Math. Soc. 367(10) (2015), 7343–7372.10.1090/S0002-9947-2014-06324-1CrossRefGoogle Scholar
4Anane, A. and Tsouli, N., On the second eigenvalue of the p-Laplacian, in Nonlinear partial differential equations, Pitman Research Notes in Mathematics Series, Volume 343, pp. 1–9 (Longman, 1996).Google Scholar
5Barile, S. and Figueiredo, G. M., Some classes of eigenvalues problems for generalized p&q-Laplacian type operators on bounded domains, Nonlinear Anal. 119 (2015), 457–468.10.1016/j.na.2014.11.002CrossRefGoogle Scholar
6Benci, V., d'Avenia, P., Fortunato, D. and Pisani, L., Solitons in several space dimensions: Derrick's problem and infinitely many solutions, Arch. Rational Mech. Anal. 154(4) (2000), 297–324.10.1007/s002050000101CrossRefGoogle Scholar
7Brézis, H., Functional analysis, Sobolev spaces and partial differential equations (Springer, 2011).Google Scholar
8Drábek, P., The p-Laplacian – mascot of nonlinear analysis, Acta Math. Univ. Comenianae 76(1) (2007), 85–98.Google Scholar
9Drábek, P. and Robinson, S. B., Resonance problems for the p-Laplacian, J. Funct. Anal. 169(1) (1999), 189–200.10.1006/jfan.1999.3501CrossRefGoogle Scholar
10Fărcăşeanu, M., Mihăilescu, M. and Stancu-Dumitru, D., On the set of eigenvalues of some PDEs with homogeneous Neumann boundary condition, Nonlinear Anal. 116 (2015), 19–25.10.1016/j.na.2014.12.019CrossRefGoogle Scholar
11Friedlander, L., Asymptotic behaviour of the eigenvalues of the p-Laplacian, Comm. Partial Differential Equations 14(8–9) (1989), 1059–1069.10.1080/03605308908820643CrossRefGoogle Scholar
12Friedman, A., Partial differential equations of parabolic type (Krieger Publishing Company, 1983).Google Scholar
13Garcia-Azorero, J. P. and Alonso, I. P., Existence and nonuniqueness for the p-Laplacian, Comm. Partial Differential Equations 12(12) (1987), 126–202.10.1080/03605308708820534CrossRefGoogle Scholar
14Henrot, A., Extremum problems for eigenvalues of elliptic operators (Springer Science and Business Media, 2006).10.1007/3-7643-7706-2CrossRefGoogle Scholar
15Lê, An, Eigenvalue problems for the p-Laplacian, Nonlinear Anal. 64(5) (2006), 1057–1099.10.1016/j.na.2005.05.056CrossRefGoogle Scholar
16Mihăilescu, M., An eigenvalue problem possessing a continuous family of eigenvalues plus an isolated eigenvalue, Commun. Pure Appl. Anal 10 (2011), 701–708.10.3934/cpaa.2011.10.701CrossRefGoogle Scholar
17Motreanu, D., Motreanu, V. V. and Papageorgiou, N., Topological and variational methods with applications to nonlinear boundary value problems (Springer, 2014).10.1007/978-1-4614-9323-5CrossRefGoogle Scholar
18Papageorgiou, N. S. and Rădulescu, V. D., Resonant (p, 2)-equations with asymmetric reaction, Anal. Appl. 13(5) (2015), 481–506.CrossRefGoogle Scholar
19Papageorgiou, N. S. and Winkert, P., Resonant (p, 2)-equations with concave terms, Appl. Anal. 94(2) (2015), 341–359.10.1080/00036811.2014.895332CrossRefGoogle Scholar
20Rellich, F., Ein Satz über mittlere Konvergenz, Nachr. Gesellsch. Wiss. Göttingen. Math.-Phys. Kl. 1930 (1930), 30–35.Google Scholar
21Robinson, S. B., On the average value for nonconstant eigenfunctions of the p-Laplacian assuming Neumann boundary data, Electron. J. Differ. Equ. Conf. 10 (2003), 251–256.Google Scholar
22Stekloff, W., Sur les problèmes fondamentaux de la physique mathématique, Ann. Sci. École Norm. Sup. 19 (1902), 191–259 and 455–490.10.24033/asens.510CrossRefGoogle Scholar
23Struwe, M., Variational methods: Applications to nonlinear partial differential equations and Hamiltonian systems (Springer, 1990).10.1007/978-3-662-02624-3CrossRefGoogle Scholar
24Tanaka, M., Generalized eigenvalue problems for (p, q)-Laplacian with indefinite weight, J. Math. Anal. Appl. 419(2) (2014), 1181–1192.10.1016/j.jmaa.2014.05.044CrossRefGoogle Scholar