Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Robinson, D. C.
2019.
Gravitation and general relativity at King’s College London.
The European Physical Journal H,
Vol. 44,
Issue. 3,
p.
181.


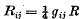 are satisfied, shows how to define at any world-point a set of principal directions intrinsically related to the Riemann tensor
are satisfied, shows how to define at any world-point a set of principal directions intrinsically related to the Riemann tensor 