No CrossRef data available.
Article contents
Fourier transforms related to ζ(s)
Published online by Cambridge University Press: 30 April 2021
Abstract
Using some formulas of S. Ramanujan, we compute in closed form the Fourier transform of functions related to Riemann zeta function $\zeta (s)=\sum \nolimits _{n=1}^{\infty } {1}/{n^{s}}$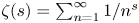 and other Dirichlet series.
and other Dirichlet series.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
Báez-Duarte, L., A strengthening of the Nyman-Beurling criterion for the Riemann Hypothesis, Atti Acad. Naz. Lincei Rend. Lincei Mat. Appl. 14 (2003), 5–11.Google Scholar
Báez-Duarte, L., Balazard, M., Landreau, B. and Saias, E., Notes sur la fonction $\zeta$ de Riemann III, Adv. Math. 149 (2000), 130–144.CrossRefGoogle Scholar
de Riemann III, Adv. Math. 149 (2000), 130–144.CrossRefGoogle Scholar
Beurling, A., A closure problem related to the Riemann zeta-function, Proc. Nat. Acad. Sci. 41 (1955), 312–314.CrossRefGoogle ScholarPubMed
Dimitrov, Dimitar K. and Rusev, Peter K., Zeros of entire Fourier Transforms, East J. Approx. 17(1) (2011), 1–110.Google Scholar
Dimitrov, Dimitar K. and Xu, Y., Wronskians of Fourier and Laplace transforms, Trans. Amer.Math. Soc. 372 (2019), 4107–4125.CrossRefGoogle Scholar
Nyman, B., On Some Groups and Semigroups of Translations, Thesis (Uppsala, 1950).Google Scholar
Panzone, P. A., Formulas for the Riemann Zeta-function and certain Dirichlet series, Int. Trans. Special Funct. 29 (2018), 893–908.CrossRefGoogle Scholar
van der Pol, B., An electro-mechanical investigation of the Riemann zeta function in the critical strip, Bull. Amer. Math. Soc. 53 (1947), 976–981.CrossRefGoogle Scholar
Ramanujan, S., Collected Papers (Cambridge University Press, Cambridge, 1927). reprinted by Chelsea, New York, 1962; reprinted by the AMS (Providence, RI, 2000).Google Scholar
Titchmarsh, E. C., The theory of Riemann Zeta-Function, edited and with a preface by D. R. Heath-Brown (Oxford Science Publications, 1986).Google Scholar



