Article contents
Fourier restriction in low fractal dimensions
Published online by Cambridge University Press: 30 April 2021
Abstract
Let $S \subset \mathbb {R}^{n}$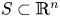 be a smooth compact hypersurface with a strictly positive second fundamental form, $E$
be a smooth compact hypersurface with a strictly positive second fundamental form, $E$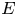 be the Fourier extension operator on $S$
be the Fourier extension operator on $S$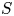 , and $X$
, and $X$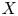 be a Lebesgue measurable subset of $\mathbb {R}^{n}$
be a Lebesgue measurable subset of $\mathbb {R}^{n}$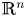 . If $X$
. If $X$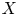 contains a ball of each radius, then the problem of determining the range of exponents $(p,q)$
contains a ball of each radius, then the problem of determining the range of exponents $(p,q)$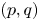 for which the estimate $\| Ef \|_{L^{q}(X)} \lesssim \| f \|_{L^{p}(S)}$
for which the estimate $\| Ef \|_{L^{q}(X)} \lesssim \| f \|_{L^{p}(S)}$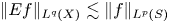 holds is equivalent to the restriction conjecture. In this paper, we study the estimate under the following assumption on the set $X$
holds is equivalent to the restriction conjecture. In this paper, we study the estimate under the following assumption on the set $X$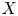 : there is a number $0 < \alpha \leq n$
: there is a number $0 < \alpha \leq n$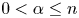 such that $|X \cap B_R| \lesssim R^{\alpha }$
such that $|X \cap B_R| \lesssim R^{\alpha }$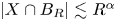 for all balls $B_R$
for all balls $B_R$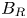 in $\mathbb {R}^{n}$
in $\mathbb {R}^{n}$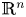 of radius $R \geq 1$
of radius $R \geq 1$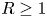 . On the left-hand side of this estimate, we are integrating the function $|Ef(x)|^{q}$
. On the left-hand side of this estimate, we are integrating the function $|Ef(x)|^{q}$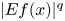 against the measure $\chi _X \,{\textrm {d}}x$
against the measure $\chi _X \,{\textrm {d}}x$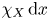 . Our approach consists of replacing the characteristic function $\chi _X$
. Our approach consists of replacing the characteristic function $\chi _X$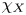 of $X$
of $X$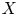 by an appropriate weight function $H$
by an appropriate weight function $H$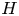 , and studying the resulting estimate in three different regimes: small values of $\alpha$
, and studying the resulting estimate in three different regimes: small values of $\alpha$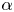 , intermediate values of $\alpha$
, intermediate values of $\alpha$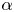 , and large values of $\alpha$
, and large values of $\alpha$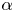 . In the first regime, we establish the estimate by using already available methods. In the second regime, we prove a weighted Hölder-type inequality that holds for general non-negative Lebesgue measurable functions on $\mathbb {R}^{n}$
. In the first regime, we establish the estimate by using already available methods. In the second regime, we prove a weighted Hölder-type inequality that holds for general non-negative Lebesgue measurable functions on $\mathbb {R}^{n}$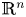 and combine it with the result from the first regime. In the third regime, we borrow a recent fractal Fourier restriction theorem of Du and Zhang and combine it with the result from the second regime. In the opposite direction, the results of this paper improve on the Du–Zhang theorem in the range $0 < \alpha < n/2$
and combine it with the result from the first regime. In the third regime, we borrow a recent fractal Fourier restriction theorem of Du and Zhang and combine it with the result from the second regime. In the opposite direction, the results of this paper improve on the Du–Zhang theorem in the range $0 < \alpha < n/2$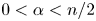 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
- 3
- Cited by



