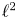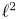1. Introduction
The $\ell ^{2}$![]() -Betti numbers were introduced by Atiyah as dimensions of heat kernels of certain operators on Riemannian manifolds. The modern formulation assigns $\ell ^{2}$
-Betti numbers were introduced by Atiyah as dimensions of heat kernels of certain operators on Riemannian manifolds. The modern formulation assigns $\ell ^{2}$![]() -Betti numbers $b^{(2)}_i(G)$
-Betti numbers $b^{(2)}_i(G)$![]() to arbitrary groups $G$
to arbitrary groups $G$![]() . We refer the reader to Lück's account where the history can be found in the introduction of [Reference Lück12]. Technical results about $\ell ^{2}$
. We refer the reader to Lück's account where the history can be found in the introduction of [Reference Lück12]. Technical results about $\ell ^{2}$![]() -Betti numbers that we need can be found in chapters 6 and 8 of loc. cit. The $\ell ^{2}$
-Betti numbers that we need can be found in chapters 6 and 8 of loc. cit. The $\ell ^{2}$![]() -Euler characteristic $\chi ^{(2)}(G)$
-Euler characteristic $\chi ^{(2)}(G)$![]() is defined to be the alternating sum of these Betti numbers when this series is absolutely convergent. Let $\mathfrak {C}$
is defined to be the alternating sum of these Betti numbers when this series is absolutely convergent. Let $\mathfrak {C}$![]() denote the class of groups $F$
denote the class of groups $F$![]() such that
such that
• $\sum \nolimits _{i\geq 0}b^{(2)}_i(G)$
 is finite (this being the condition for absolute convergence),
is finite (this being the condition for absolute convergence),• $b^{(2)}_1(F)=b^{(2)}_2(F)=0$
 , and
, and• either $\chi ^{(2)}(F)=0$
 or $F$
or $F$ is finite.
is finite.
Note that $\mathfrak {C}$![]() contains all $\ell ^{2}$
contains all $\ell ^{2}$![]() -acyclic groups (i.e. the groups for which $b_i^{(2)}=0$
-acyclic groups (i.e. the groups for which $b_i^{(2)}=0$![]() for all $i>0$
for all $i>0$![]() ) and, in particular, it contains all amenable groups. Relevant background on $\ell ^{2}$
) and, in particular, it contains all amenable groups. Relevant background on $\ell ^{2}$![]() -cohomology is included in § 2. In this note, we prove the following theorem.
-cohomology is included in § 2. In this note, we prove the following theorem.
Theorem 1.1 Let $F$![]() be a group acting simplicially and cocompactly on a simplicial tree, with vertex and edge stabilizers in $\mathfrak {C},$
be a group acting simplicially and cocompactly on a simplicial tree, with vertex and edge stabilizers in $\mathfrak {C},$![]() let $N$
let $N$![]() be a subgroup normally generated by $m$
be a subgroup normally generated by $m$![]() elements, intersecting the vertex stabilizers trivially, and let $G$
elements, intersecting the vertex stabilizers trivially, and let $G$![]() denote $F/N$
denote $F/N$![]() . Then $\chi ^{(2)}(F)$
. Then $\chi ^{(2)}(F)$![]() is defined and setting $k:=\chi ^{(2)}(F)+m$
is defined and setting $k:=\chi ^{(2)}(F)+m$![]() the following conclusions hold:
the following conclusions hold:
(i) If $k\leq 0,$
 then $G$
then $G$ is infinite.
is infinite.(ii) If $k < 0,$
 then $b^{(2)}_1(G)\geq -k >0$
then $b^{(2)}_1(G)\geq -k >0$ .
.(iii) If $G$
 is finite, then $k>0$
is finite, then $k>0$ and $|G|\geq \frac {1}{k}$
and $|G|\geq \frac {1}{k}$ .
.
Note that the hypotheses of this theorem guarantee that $N$![]() acts freely on the specified tree and, in particular, $N$
acts freely on the specified tree and, in particular, $N$![]() is necessarily a free group. Note also that, according to [Reference Bader, Furman and Sauer2, Corollary 1.4], if $b^{(2)}_1(G)>0$
is necessarily a free group. Note also that, according to [Reference Bader, Furman and Sauer2, Corollary 1.4], if $b^{(2)}_1(G)>0$![]() then $G$
then $G$![]() has no commensurated infinite amenable subgroup and according to [Reference Bekka and Valette3, Corollary 6] does not have property (T). If we also have $b_2^{(2)}(G)=0$
has no commensurated infinite amenable subgroup and according to [Reference Bekka and Valette3, Corollary 6] does not have property (T). If we also have $b_2^{(2)}(G)=0$![]() , then $G$
, then $G$![]() is in the class $\mathcal {D}_\textrm {reg}$
is in the class $\mathcal {D}_\textrm {reg}$![]() by [Reference Thom15, Lemma 2.8]. We refer the reader to [Reference Bekka, de la Harpe and Valette4] for background on property (T) and to [Reference Thom15, Definition 2.6] for the definition of the class $\mathcal {D}_{\mathrm {reg}}$
by [Reference Thom15, Lemma 2.8]. We refer the reader to [Reference Bekka, de la Harpe and Valette4] for background on property (T) and to [Reference Thom15, Definition 2.6] for the definition of the class $\mathcal {D}_{\mathrm {reg}}$![]() . Acylindrically hyperbolic groups form a large class of groups admitting coarsely proper actions on hyperbolic metric spaces. The class is a generalization of relative hyperbolicity including many Artin groups, mapping class groups, and $\mathrm {Out}(F_n)$
. Acylindrically hyperbolic groups form a large class of groups admitting coarsely proper actions on hyperbolic metric spaces. The class is a generalization of relative hyperbolicity including many Artin groups, mapping class groups, and $\mathrm {Out}(F_n)$![]() . By the main result of Osin's paper [Reference Osin13], we have the following corollary.
. By the main result of Osin's paper [Reference Osin13], we have the following corollary.
Corollary 1.2 Let $G,$![]() $F$
$F$![]() and $N$
and $N$![]() be as in Theorem 1.1. Assume that $G$
be as in Theorem 1.1. Assume that $G$![]() is finitely presented, (virtually) indicable and that $\chi ^{(2)}(F)+m<0$
is finitely presented, (virtually) indicable and that $\chi ^{(2)}(F)+m<0$![]() . Then $G$
. Then $G$![]() is (virtually) acylindrically hyperbolic.
is (virtually) acylindrically hyperbolic.
The simplest way in which the indicability hypothesis may arise is through stable letters: Let $T$![]() denote the $F$
denote the $F$![]() -tree of Theorem 1.1. Let $K$
-tree of Theorem 1.1. Let $K$![]() denote the (necessarily normal) subgroup generated by the vertex stabilizers. Then there is a subgroup $E\le F$
denote the (necessarily normal) subgroup generated by the vertex stabilizers. Then there is a subgroup $E\le F$![]() that complements $K$
that complements $K$![]() and all such subgroups are free of uniquely determined rank. Such a subgroup may be referred to as a subgroup of stable letters of the action. The group $G$
and all such subgroups are free of uniquely determined rank. Such a subgroup may be referred to as a subgroup of stable letters of the action. The group $G$![]() has an infinite cyclic quotient when $N\cap E$
has an infinite cyclic quotient when $N\cap E$![]() has infinite index in $E$
has infinite index in $E$![]() , in other words, when there is a stable letter that is faithfully represented in $G$
, in other words, when there is a stable letter that is faithfully represented in $G$![]() , and in this case, $G$
, and in this case, $G$![]() is indicable.
is indicable.
Recall that a group $G$![]() is $C^{\ast }$
is $C^{\ast }$![]() -simple if the reduced group $C^{\ast }$
-simple if the reduced group $C^{\ast }$![]() -algebra, denoted $C_r^{\ast }(G)$
-algebra, denoted $C_r^{\ast }(G)$![]() , has exactly two norm closed $2$
, has exactly two norm closed $2$![]() -sided ideals, $0$
-sided ideals, $0$![]() , and the algebra $C_r^{\ast }(G)$
, and the algebra $C_r^{\ast }(G)$![]() itself. By [Reference Breuillard, Kalantar, Kennedy and Ozawa5, Corollary 6.7], we obtain the following.
itself. By [Reference Breuillard, Kalantar, Kennedy and Ozawa5, Corollary 6.7], we obtain the following.
Corollary 1.3 Let $G,$![]() $F$
$F$![]() and $N$
and $N$![]() be as in Theorem 1.1. Then $G$
be as in Theorem 1.1. Then $G$![]() is $C^{\ast }$
is $C^{\ast }$![]() -simple if and only if it has trivial amenable radical.
-simple if and only if it has trivial amenable radical.
These two corollaries highlight the relation between the first $\ell ^{2}$![]() -Betti number and other areas of geometric group theory. It is an interesting matter for further research to find out whether they lead to new examples.
-Betti number and other areas of geometric group theory. It is an interesting matter for further research to find out whether they lead to new examples.
Theorem 1.1 has some historical pedigree. It originally began life as a result about quotients of free groups due to Thomas (see Theorem 1.4(i)) and was proved using combinatorial methods [Reference Thomas16]. The result was generalized by Allcock to incorporate a bound on the rank of the abelianisation of the quotient group [Reference Allcock1]. The introduction of $\ell ^{2}$![]() -cohomology came when Peterson–Thom [Reference Peterson and Thom14, Theorem 3.6] and Kar–Niblo [Reference Kar and Niblo11] independently linked the inequality of Thomas to the first $\ell ^{2}$
-cohomology came when Peterson–Thom [Reference Peterson and Thom14, Theorem 3.6] and Kar–Niblo [Reference Kar and Niblo11] independently linked the inequality of Thomas to the first $\ell ^{2}$![]() -Betti number. These discoveries are summarized in the following result.
-Betti number. These discoveries are summarized in the following result.
Theorem 1.4 (Thomas [Reference Thomas16], Allcock [Reference Allcock1], Peterson–Thom [Reference Peterson and Thom14], Kar–Niblo [Reference Kar and Niblo11])
Let $G$![]() be a group with a presentation
be a group with a presentation
in which the elements $r_{i}$![]() have order $k_{i}$
have order $k_{i}$![]() when interpreted in $G$
when interpreted in $G$![]() .
.
(i) If $n-\sum \nolimits _{i=1}^{m}\frac 1{k_{i}}\ge 1$
 then $G$
then $G$ is infinite.
is infinite.(ii) If $G$
 is finite then $|G|\ge \frac 1{1-n+\sum \nolimits _{i=1}^{m}k_{i}}$
is finite then $|G|\ge \frac 1{1-n+\sum \nolimits _{i=1}^{m}k_{i}}$ .
.(iii) If $n-\sum \nolimits _{i=1}^{m}\frac 1{k_{i}} > 1$
 then $G$
then $G$ is non-amenable.
is non-amenable.
Deduction of Theorem 1.4 from Theorem 1.1 Let $G$![]() be a group with a presentation
be a group with a presentation
Adding $m$![]() fresh generators $y_{1},\,\dots,\,y_{m}$
fresh generators $y_{1},\,\dots,\,y_{m}$![]() , we can give the following alternative presentation of the same group:
, we can give the following alternative presentation of the same group:
Let $F$![]() be the group with presentation
be the group with presentation
and let $N$![]() be the subgroup of $F$
be the subgroup of $F$![]() normally generated by $r_{1}y_{1}^{-1},\,\dots,\,r_{m}y_{m}^{-1}$
normally generated by $r_{1}y_{1}^{-1},\,\dots,\,r_{m}y_{m}^{-1}$![]() . Then $F$
. Then $F$![]() is a free product of cyclic groups which has a natural action on a simplicial tree $T$
is a free product of cyclic groups which has a natural action on a simplicial tree $T$![]() (the Bass–Serre tree). In particular, it is virtually free and has Euler characteristic $\chi (F)=\sum \nolimits _{i=1}^{m}\frac 1{k_{i}}-n-m+1$
(the Bass–Serre tree). In particular, it is virtually free and has Euler characteristic $\chi (F)=\sum \nolimits _{i=1}^{m}\frac 1{k_{i}}-n-m+1$![]() (as explained in [Reference Brown6, Chapter IX.7]). This is equal to $\chi ^{(2)}(F)$
(as explained in [Reference Brown6, Chapter IX.7]). This is equal to $\chi ^{(2)}(F)$![]() by [Reference Lück12, Remark 6.81]. The condition that the $r_{i}$
by [Reference Lück12, Remark 6.81]. The condition that the $r_{i}$![]() have order $k_{i}$
have order $k_{i}$![]() in the original presentation ensures that $N$
in the original presentation ensures that $N$![]() does not meet any of the finite subgroups of $F$
does not meet any of the finite subgroups of $F$![]() , so is torsion-free and acts freely on $T$
, so is torsion-free and acts freely on $T$![]() . Applying Theorem 1.1 with these choices of $F$
. Applying Theorem 1.1 with these choices of $F$![]() , $N$
, $N$![]() , $G$
, $G$![]() and $T$
and $T$![]() yields Theorem 1.4.
yields Theorem 1.4.
Throughout this paper, for a group or subgroup $G$![]() , we will adopt the convention that $\frac {1}{|G|}$
, we will adopt the convention that $\frac {1}{|G|}$![]() be interpreted as zero if $G$
be interpreted as zero if $G$![]() is infinite.
is infinite.
Finally, we compute the first $\ell ^{2}$![]() -Betti number for certain groups acting on trees leading to Theorem 1.5 below, which is proved in § 4. This generalizes a result of Lück [Reference Brown, Dykema and Jung7], which covers the case of an amalgamated free product, and a result of Tsouvalas [Reference Tsouvalas17, Corollary 3.7]. Tsouvalas assumes the vertex stabilisers are either residually finite or virtually torsion-free and the edge stabilisers are finite. Here we replace both of these assumptions with Lück's less restrictive assumption that the first $\ell ^{2}$
-Betti number for certain groups acting on trees leading to Theorem 1.5 below, which is proved in § 4. This generalizes a result of Lück [Reference Brown, Dykema and Jung7], which covers the case of an amalgamated free product, and a result of Tsouvalas [Reference Tsouvalas17, Corollary 3.7]. Tsouvalas assumes the vertex stabilisers are either residually finite or virtually torsion-free and the edge stabilisers are finite. Here we replace both of these assumptions with Lück's less restrictive assumption that the first $\ell ^{2}$![]() -Betti numbers of the edge stabilisers vanish. So, for example, the theorem applies to fundamental groups of graphs of $\mathfrak {C}$
-Betti numbers of the edge stabilisers vanish. So, for example, the theorem applies to fundamental groups of graphs of $\mathfrak {C}$![]() -groups.
-groups.
Theorem 1.5 Let $F$![]() be a group acting simplicially on a simplicial tree and let $V$
be a group acting simplicially on a simplicial tree and let $V$![]() and $E$
and $E$![]() denote sets of representatives of $F$
denote sets of representatives of $F$![]() -orbits of vertices and edges. Assume for each $e\in E$
-orbits of vertices and edges. Assume for each $e\in E$![]() that $b^{(2)}_1(F_e)=0,$
that $b^{(2)}_1(F_e)=0,$![]() then we have
then we have

2. Background on ${\ell ^{2}}$ -homology
-homology
Let $G$![]() be a group. Then both $G$
be a group. Then both $G$![]() and the complex group algebra $\mathbb {C} G$
and the complex group algebra $\mathbb {C} G$![]() act by left multiplication on the Hilbert space $\ell ^{2}G$
act by left multiplication on the Hilbert space $\ell ^{2}G$![]() of square-summable sequences. The group von Neumann algebra $\mathcal {N}G$
of square-summable sequences. The group von Neumann algebra $\mathcal {N}G$![]() is the ring of $G$
is the ring of $G$![]() -equivariant bounded operators on $\ell ^{2}G$
-equivariant bounded operators on $\ell ^{2}G$![]() . The regular elements of $\mathcal {N}G$
. The regular elements of $\mathcal {N}G$![]() form an Ore set and the Ore localization of $\mathcal {N}G$
form an Ore set and the Ore localization of $\mathcal {N}G$![]() can be identified with the ring of affiliated operators, and is denoted by $\mathcal {U}G$
can be identified with the ring of affiliated operators, and is denoted by $\mathcal {U}G$![]() . One has the inclusions $\mathbb {C} G\subseteq \mathcal {N} G\subseteq \ell ^{2}G\subseteq \mathcal {U}G$
. One has the inclusions $\mathbb {C} G\subseteq \mathcal {N} G\subseteq \ell ^{2}G\subseteq \mathcal {U}G$![]() and it is also known that $\mathcal {U}G$
and it is also known that $\mathcal {U}G$![]() is a self-injective ring which is flat over $\mathcal {N}G$
is a self-injective ring which is flat over $\mathcal {N}G$![]() . For more details concerning these constructions, we refer the reader to [Reference Lück12] and especially to Theorem 8.22 of § 8.2.3 therein. The von Neumann dimension and the basic properties we need can be found in [Reference Lück12, § 8.3]. Now let $Y$
. For more details concerning these constructions, we refer the reader to [Reference Lück12] and especially to Theorem 8.22 of § 8.2.3 therein. The von Neumann dimension and the basic properties we need can be found in [Reference Lück12, § 8.3]. Now let $Y$![]() be a $G$
be a $G$![]() -CW complex as defined in [Reference Lück12, Definition 1.25 of § 1.2]. The $\ell ^{2}$
-CW complex as defined in [Reference Lück12, Definition 1.25 of § 1.2]. The $\ell ^{2}$![]() -homology groups of $Y$
-homology groups of $Y$![]() are then defined to be the equivariant homology groups $H^{G}_i(Y;\mathcal {U}G)$
are then defined to be the equivariant homology groups $H^{G}_i(Y;\mathcal {U}G)$![]() , and we have
, and we have
The $\ell ^{2}$![]() -Betti numbers of a group $G$
-Betti numbers of a group $G$![]() are then defined to be the $\ell ^{2}$
are then defined to be the $\ell ^{2}$![]() -Betti numbers of $EG$
-Betti numbers of $EG$![]() , that is to say
, that is to say
By [Reference Lück12, Theorem 6.54(8)], the zeroeth $\ell ^{2}$![]() -Betti number of $G$
-Betti number of $G$![]() is equal to $1/|G|$
is equal to $1/|G|$![]() . Moreover, if $G$
. Moreover, if $G$![]() is finite then $b_n^{(2)}(G)=0$
is finite then $b_n^{(2)}(G)=0$![]() for $n\geq 1$
for $n\geq 1$![]() .
.
Let $C_*(Y;\mathcal {U}G)$![]() denote the standard cellular chain complex of $Y$
denote the standard cellular chain complex of $Y$![]() with coefficients in $\mathcal {U}G$
with coefficients in $\mathcal {U}G$![]() . We have the formula
. We have the formula
where $\sigma$![]() runs through a set of orbit representatives of $i$
runs through a set of orbit representatives of $i$![]() -dimensional cells in $Y$
-dimensional cells in $Y$![]() . Suppose that the $\ell ^{2}$
. Suppose that the $\ell ^{2}$![]() -Euler characteristic of $Y$
-Euler characteristic of $Y$![]() is defined. Standard arguments of homological algebra give the connection between two Euler characteristic computations (for the details see [Reference Lück12, Lemma 6.80(1)]):
is defined. Standard arguments of homological algebra give the connection between two Euler characteristic computations (for the details see [Reference Lück12, Lemma 6.80(1)]):
We will need the following lemma for the proofs in the next section. One should think of it as a mild generalization of Theorem 6.54(2) in [Reference Lück12].
Lemma 2.1 Comparison with the Borel construction up to rank
Let $X$![]() be a $G$
be a $G$![]() -CW complex. Suppose for all $x\in X$
-CW complex. Suppose for all $x\in X$![]() the isotropy group $G_x$
the isotropy group $G_x$![]() is finite or $b^{(2)}_p(G_x)=0$
is finite or $b^{(2)}_p(G_x)=0$![]() for all $0\leq p \leq n,$
for all $0\leq p \leq n,$![]() then
then
Proof. It suffices to prove that the von Neumann dimensions of the kernel and cokernel of the map
induced by the projection $EG\times X\rightarrow X$![]() are zero for $0\leq p \leq n$
are zero for $0\leq p \leq n$![]() . Here $EG\times X$
. Here $EG\times X$![]() carries the diagonal action of $G$
carries the diagonal action of $G$![]() . By an identical argument to [Reference Lück12, Theorem 6.54(2)], it suffices to prove for each isotropy subgroup $H\leq G$
. By an identical argument to [Reference Lück12, Theorem 6.54(2)], it suffices to prove for each isotropy subgroup $H\leq G$![]() and $0\leq p \leq n$
and $0\leq p \leq n$![]() the kernel and cokernel of the map $\textrm {pr}_p:H^{H}_p(EH;\mathcal {U}H)\rightarrow H^{H}_p(\ast ;\mathcal {U}H)$
the kernel and cokernel of the map $\textrm {pr}_p:H^{H}_p(EH;\mathcal {U}H)\rightarrow H^{H}_p(\ast ;\mathcal {U}H)$![]() have dimension equal to zero. If $H$
have dimension equal to zero. If $H$![]() is finite this follows from [Reference Lück12, Theorem 6.54(8a)], and is immediate if $b^{(2)}_p(H)=0$
is finite this follows from [Reference Lück12, Theorem 6.54(8a)], and is immediate if $b^{(2)}_p(H)=0$![]() for all $0\leq p \leq n$
for all $0\leq p \leq n$![]() .
.
3. The main theorem
To prove Theorem 1.1, one needs the following method of computing the $\ell ^{2}$![]() -Euler characteristic of a group acting on a tree analogous to Chiswell's result [Reference Chiswell9] for rational Euler characteristic.
-Euler characteristic of a group acting on a tree analogous to Chiswell's result [Reference Chiswell9] for rational Euler characteristic.
Proposition 3.1 (Chatterji–Mislin [Reference Chatterji and Mislin8])
Let $F$![]() be a group acting on a tree and let $V$
be a group acting on a tree and let $V$![]() and $E$
and $E$![]() denote sets of representatives of $F$
denote sets of representatives of $F$![]() -orbits of vertices and edges. If the $\ell ^{2}$
-orbits of vertices and edges. If the $\ell ^{2}$![]() -Euler characteristic of each vertex and edge group is finite, then
-Euler characteristic of each vertex and edge group is finite, then
Proof of Theorem 1.1. There is a cocompact action of $F$![]() on a tree $T$
on a tree $T$![]() with vertex and edge stabilisers in the class $\mathfrak {C}$
with vertex and edge stabilisers in the class $\mathfrak {C}$![]() . Let $V$
. Let $V$![]() and $E$
and $E$![]() denote the vertex and edge sets. Let $\overline T$
denote the vertex and edge sets. Let $\overline T$![]() denote the quotient graph $T/N$
denote the quotient graph $T/N$![]() and write $\overline V$
and write $\overline V$![]() and $\overline E$
and $\overline E$![]() for its vertex and edge sets. Now $G=F/N$
for its vertex and edge sets. Now $G=F/N$![]() acts cocompactly on $\overline T$
acts cocompactly on $\overline T$![]() with vertex and edge stabilizers in $\mathfrak {C}$
with vertex and edge stabilizers in $\mathfrak {C}$![]() . The augmented chain complex of $T$
. The augmented chain complex of $T$![]() is the short exact sequence
is the short exact sequence
of $\mathbb {Z} F$![]() -modules. Restricting to the action of $N$
-modules. Restricting to the action of $N$![]() this short exact sequence leads to a long exact sequence for the homology of $N$
this short exact sequence leads to a long exact sequence for the homology of $N$![]() . It is straightforward to identify $H_0(N;\mathbb {Z} V)$
. It is straightforward to identify $H_0(N;\mathbb {Z} V)$![]() with $\mathbb {Z} \overline V$
with $\mathbb {Z} \overline V$![]() and $H_0(N;\mathbb {Z} E)$
and $H_0(N;\mathbb {Z} E)$![]() with $\mathbb {Z} \overline E$
with $\mathbb {Z} \overline E$![]() , so that the tail end of the sequence takes the form
, so that the tail end of the sequence takes the form
Let $\{r_i\colon i=1,\,..m\}$![]() denote a normal generating set for $N$
denote a normal generating set for $N$![]() . Choose a vertex $v_{0}$
. Choose a vertex $v_{0}$![]() in $T$
in $T$![]() to be a fixed basepoint. For $1\le i\le m$
to be a fixed basepoint. For $1\le i\le m$![]() , consider the geodesic from $v_{0}$
, consider the geodesic from $v_{0}$![]() to $v_{0}r_{i}$
to $v_{0}r_{i}$![]() . In the quotient graph $\overline T$
. In the quotient graph $\overline T$![]() , this geodesic descends to a loop because $v_{0}$
, this geodesic descends to a loop because $v_{0}$![]() and $v_{0}r_{i}$
and $v_{0}r_{i}$![]() become identified in $\overline T$
become identified in $\overline T$![]() . Now $2$
. Now $2$![]() -discs can be glued to each loop. By adjoining free $G$
-discs can be glued to each loop. By adjoining free $G$![]() -orbits of $2$
-orbits of $2$![]() -discs equivariantly, we can build a $2$
-discs equivariantly, we can build a $2$![]() -complex $Y$
-complex $Y$![]() with an action of $G$
with an action of $G$![]() , whose $1$
, whose $1$![]() -skeleton is $\overline T$
-skeleton is $\overline T$![]() , and which has augmented cellular chain complex
, and which has augmented cellular chain complex
By construction the map $\mathbb {Z} G^{m}\to \mathbb {Z}\overline E$![]() factors through a surjection $\mathbb {Z} G^{m}\to H_1(N;\mathbb {Z})$
factors through a surjection $\mathbb {Z} G^{m}\to H_1(N;\mathbb {Z})$![]() . Therefore, the exactness of (3) ensures the exactness of (4). It follows that $Y$
. Therefore, the exactness of (3) ensures the exactness of (4). It follows that $Y$![]() is $1$
is $1$![]() -acyclic.
-acyclic.
Let $V_{0}$![]() and $E_{0}$
and $E_{0}$![]() be sets of orbit representatives of vertices and edges in $Y$
be sets of orbit representatives of vertices and edges in $Y$![]() . Now, applying Proposition 3.1 then (2), we have that
. Now, applying Proposition 3.1 then (2), we have that

Lemma 2.1 with $n=2$![]() , yields
, yields

Applying [Reference Lück12, Theorem 6.54(1a)] to the projection $f:EG\times Y\rightarrow EG$![]() with $n=2$
with $n=2$![]() (note that we are using the fact $Y$
(note that we are using the fact $Y$![]() is $1$
is $1$![]() -acyclic), we obtain $b^{(2)}_i(EG\times Y)=b^{(2)}_i(EG)$
-acyclic), we obtain $b^{(2)}_i(EG\times Y)=b^{(2)}_i(EG)$![]() for $i=0,\,1$
for $i=0,\,1$![]() . Recalling (1), we therefore have
. Recalling (1), we therefore have
Let $k=\chi ^{(2)}(F)+m$![]() . If $k\leq 0$
. If $k\leq 0$![]() , then $b^{(2)}_{0}(G)- b^{(2)}_{1}(G)\leq 0$
, then $b^{(2)}_{0}(G)- b^{(2)}_{1}(G)\leq 0$![]() and so $G$
and so $G$![]() is infinite, this proves (i). Now, assume $k<0$
is infinite, this proves (i). Now, assume $k<0$![]() . In this case, $G$
. In this case, $G$![]() is infinite and therefore $b^{(2)}_{0}(G)=0$
is infinite and therefore $b^{(2)}_{0}(G)=0$![]() . It follows that $b^{(2)}_{1}(G)\geq -k>0$
. It follows that $b^{(2)}_{1}(G)\geq -k>0$![]() , this proves (ii).
, this proves (ii).
If $G$![]() is finite, then $b^{(2)}_0(G)=\frac {1}{|G|}$
is finite, then $b^{(2)}_0(G)=\frac {1}{|G|}$![]() , $b^{(2)}_1(G)=0$
, $b^{(2)}_1(G)=0$![]() , and $k>0$
, and $k>0$![]() . In particular, $k\geq \frac {1}{|G|}>0$
. In particular, $k\geq \frac {1}{|G|}>0$![]() and (iii) follows.
and (iii) follows.
4. On the $\ell ^{2}$ -invariants for certain groups acting on trees
-invariants for certain groups acting on trees
Proof of Theorem 1.5 Let $V$![]() and $E$
and $E$![]() denote sets of representatives of $F$
denote sets of representatives of $F$![]() -orbits of vertices and edges for the action of $F$
-orbits of vertices and edges for the action of $F$![]() on the tree. We consider the relevant part of the $E^{1}$
on the tree. We consider the relevant part of the $E^{1}$![]() -page for the $F$
-page for the $F$![]() -equivariant spectral sequence (see Chapter VII.9 of [Reference Brown6]) applied to the tree:
-equivariant spectral sequence (see Chapter VII.9 of [Reference Brown6]) applied to the tree:

If $F$![]() is finite then $b_1^{(2)}(F)=0$
is finite then $b_1^{(2)}(F)=0$![]() , so $d^{1}$
, so $d^{1}$![]() is injective and $E^{2}_{1,0}=0$
is injective and $E^{2}_{1,0}=0$![]() . The result follows from the fact $E^{1}_{0,1}=0$
. The result follows from the fact $E^{1}_{0,1}=0$![]() .
.
Now, assume $F$![]() is infinite, then $d^{1}$
is infinite, then $d^{1}$![]() is surjective since $b^{(2)}_0(F)=0$
is surjective since $b^{(2)}_0(F)=0$![]() . Thus,
. Thus,
Now, the spectral sequence obviously collapses on the $E^{2}$![]() -page and $E^{1}_{0,1}=E^{2}_{0,1}$
-page and $E^{1}_{0,1}=E^{2}_{0,1}$![]() . Since von Neumann dimension is additive over short exact sequences, we have
. Since von Neumann dimension is additive over short exact sequences, we have

and the result follows.
Acknowledgements
This paper contains material from the second author's PhD thesis [Reference Hughes10]. The second author wishes to thank Ian Leary for his tireless and good humoured role as thesis adviser. The second author was supported by the Engineering and Physical Sciences Research Council grant number 2127970. We are also indebted to Kevin Li and to the anonymous referee for a number of helpful comments and corrections.