Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T20:33:40.030Z Has data issue: false hasContentIssue false
  • English
  • Français

The fibre of the degree 3 map, Anick spaces and the double suspension

Part of: Homotopy theory

Published online by Cambridge University Press:  21 July 2020

Steven Amelotte
Steven Amelotte*
Affiliation:
Department of Mathematics, University of Rochester, 915 Hylan Building, Rochester, NY14627, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let S2n+1{p} denote the homotopy fibre of the degree p self map of S2n+1. For primes p ≥ 5, work by Selick shows that S2n+1{p} admits a non-trivial loop space decomposition if and only if n = 1 or p. Indecomposability in all but these dimensions was obtained by showing that a non-trivial decomposition of ΩS2n+1{p} implies the existence of a p-primary Kervaire invariant one element of order p in 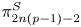$\pi _{2n(p-1)-2}^S$. We prove the converse of this last implication and observe that the homotopy decomposition problem for ΩS2n+1{p} is equivalent to the strong p-primary Kervaire invariant problem for all odd primes. For p = 3, we use the 3-primary Kervaire invariant element θ3 to give a new decomposition of ΩS55{3} analogous to Selick's decomposition of ΩS2p+1{p} and as an application prove two new cases of a long-standing conjecture stating that the fibre of the double suspension 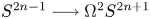$S^{2n-1} \longrightarrow \Omega ^2S^{2n+1}$ is homotopy equivalent to the double loop space of Anick's space.

Keywords

loop space decompositiondouble suspensionAnick spaceKervaire invariant

MSC classification

Primary: 55P35: Loop spaces
Secondary: 55P10: Homotopy equivalences
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 3 , August 2020 , pp. 830 - 843
Check for updates
Copyright
Copyright © The Authors, 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amelotte, S., A homotopy decomposition of the fibre of the squaring map on Ω3S 17, Homology Homotopy Appl. 20 (2018), 141–154.CrossRefGoogle Scholar
Anick, D., Differential algebras in topology, Research Notes in Mathematics (AK Peters, 1993).CrossRefGoogle Scholar
Anick, D. and Gray, B., Small H-spaces related to Moore spaces, Topology 34 (1995), 859–881.CrossRefGoogle Scholar
Campbell, H. E. A., Cohen, F. R., Peterson, F. P. and Selick, P. S., The space of maps of Moore spaces into spheres, in Proceedings of John Moore Conference on Algebraic Topology and Algebraic K-Theory, Annals of Mathematics Studies, Volume 113, pp. 72–100 (Princeton University Press, Princeton, 1987).CrossRefGoogle Scholar
Cohen, F. R., Two-primary analogues of Selick's theorem and the Kahn–Priddy theorem for the 3-sphere, Topology 23 (1984), 401–421.CrossRefGoogle Scholar
Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., Torsion in homotopy groups, Ann. of Math. 109 (1979), 121–168.CrossRefGoogle Scholar
Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., The double suspension and exponents of the homotopy groups of spheres, Ann. of Math. 110 (1979), 549–565.CrossRefGoogle Scholar
Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., Decompositions of loop spaces and applications to exponents, in Algebraic Topology, Aarhus 1978, Lecture Notes in Mathematics, Volume 763, pp. 1–12 (Springer, Berlin, 1979).CrossRefGoogle Scholar
Cohen, F. R. and Selick, P. S., Splittings of two function spaces, Q. J. Math. 41 (1990), 145–153.10.1093/qmath/41.2.145CrossRefGoogle Scholar
Gray, B., On the sphere of origin of infinite families in the homotopy groups of spheres, Topology 8 (1969), 219–232.CrossRefGoogle Scholar
Gray, B., On the iterated suspension, Topology 27 (1988), 301–310.CrossRefGoogle Scholar
Gray, B., EHP spectra and periodicity. I. Geometric constructions, Trans. Amer. Math. Soc. 340 (1993), 595–616.Google Scholar
Gray, B., Abelian properties of Anick spaces, Mem. Amer. Math. Soc. 246 (2017), 1–118.Google Scholar
Gray, B. and Theriault, S., On the double suspension and the mod-p Moore space, Contemp. Math. 399 (2006), 101–121.CrossRefGoogle Scholar
Gray, B. and Theriault, S., An elementary construction of Anick's fibration, Geom. Topol. 14 (2010), 243–275.CrossRefGoogle Scholar
Neisendorfer, J. A., 3-primary exponents, Math. Proc. Cambridge Philos. Soc. 90 (1981), 63–83.CrossRefGoogle Scholar
Neisendorfer, J. A., Properties of certain H-spaces, Q. J. Math. 34 (1983), 201–209.CrossRefGoogle Scholar
Ravenel, D. C., The non-existence of odd primary Arf invariant elements in stable homotopy, Math. Proc. Cambridge Philos. Soc. 83 (1978), 429–443.CrossRefGoogle Scholar
Ravenel, D. C., Complex cobordism and stable homotopy groups of spheres, 2nd edition, Volume 347 (AMS Chelsea Publishing, Providence, RI, 2004).Google Scholar
Selick, P. S., Odd primary torsion in πk(S 3), Topology 17 (1978), 407–412.CrossRefGoogle Scholar
Selick, P. S., A decomposition of $\pi _\ast (S^2p+1;\mathbb {Z}/p\mathbb {Z})$, Topology 20 (1981), 175–177.CrossRefGoogle Scholar
Selick, P. S., A reformulation of the Arf invariant one mod p problem and applications to atomic spaces, Pac. J. Math. 108 (1983), 431–450.CrossRefGoogle Scholar
Selick, P. S., Space exponents for loop spaces of spheres, Fields Inst. Commun. 19 (1998), 279–283.Google Scholar
Theriault, S., Properties of Anick's spaces, Trans. Amer. Math. Soc. 353 (2001), 1009–1037.CrossRefGoogle Scholar
Theriault, S., The 3-primary classifying space of the fiber of the double suspension, Proc. Amer. Math. Soc. 136 (2008), 1489–1499.10.1090/S0002-9939-07-09249-0CrossRefGoogle Scholar
Theriault, S., A case when the fiber of the double suspension is the double loops on Anick's space, Canad. Math. Bull. 53 (2010), 730–736.CrossRefGoogle Scholar