Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T20:22:10.827Z Has data issue: false hasContentIssue false
  • English
  • Français

The fibre of a cell attachment

Published online by Cambridge University Press:  20 January 2009

Stephen Halperin  and
Jean-Michel Lemaire
Stephen Halperin
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario M5S 1A1, Canada E-mail address: [email protected]
Jean-Michel Lemaire
Affiliation:
J. A. Dieudonné, URA CNRS N° 168, Université de Nice Sophia-Antipolis, F-06108 Nice Cedex 2, France E-mail address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In view of understanding the Hopf algebra structure of the loop space homology in terms of H*(ΩE) and the map f, we consider the homotopy fibre F of the inclusion map 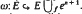In [15], the case when H*(Ωω) is surjective (the “inert” case) was studied, and in [11] a weaker condition, called “lazy”, was considered. Here we give several new characterizations of inert and lazy cell attachments in terms of properties of F. We also show how these results extend to the case of the mapping cone 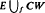of an arbitrary map f: W→E.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 38 , Issue 2 , June 1995 , pp. 295 - 311
Copyright
Copyright © Edinburgh Mathematical Society 1995

References

REFERENCES

1.Adams, J. F. and Hilton, P. J., On the chain algebra of a loop space, Comment Math. Helv. 30 (1955), 305–330.CrossRefGoogle Scholar
2.Aubry, M. and Lemaire, J.-M., Homotopies d'algèbres de Lie et de leurs algèbres enveloppantes, in Algebraic Topology & Rational Homotopy (Springer Lect. Notes Math. 1318, 1988), 26–30.CrossRefGoogle Scholar
3.Baues, H. and Lemaire, J.-M.., Minimal models in homotopy theory, Math. Ann. 225 (1977), 219–242.CrossRefGoogle Scholar
4.Bousfield, A. K. and Gugenheim, V. K. A. M., On the PL de Rham theory and rational homotopy type, Memoirs Amer. Math. Soc. 179 (1976).Google Scholar
5.Félix, Y., and Halperin, S., Rational LS category and its applications, Trans. Amer. Math. Soc. 273 (1982), 1–37.Google Scholar
6.Félix, Y., Halperin, S., Lemaire, J.-M. and Thomas, J.-C., Mod p loop space homology, Invent. Math. 95 (1989), 247–262.CrossRefGoogle Scholar
7.Félix, Y., Halperin, S. and Thomas, J.-C., Elliptic Hopf algebras, J. London Math. Soc. (2) 43 (1991), 545–555.CrossRefGoogle Scholar
8.Félix, Y., Halperin, S. and Thomas, J.-C., Hopf algebras of polynomial growth, J. Algebra 125 (1989), 408–417.CrossRefGoogle Scholar
9.Félix, Y., Halperin, S. and Thomas, J.-C., Lie algebras of polynomial growth, J. London Math. Soc. (2) 43 (1991), 556–566.CrossRefGoogle Scholar
10.Félix, Y., Halperin, S. and Thomas, J.-C., The Serre spectral sequence of a multiplicative fibration, preprint.Google Scholar
11.Félix, Y. and Lemaire, J.-M., On the Pontryagin algebra of the loops on a space with a cell attached, Internal. J. Math. 2 (1991), 429–438.Google Scholar
12.Félix, Y. and Thomas, J.-C., Module d'holonomie d'une fibration, Bull. Soc. Math. France 113 (1985), 255–258.CrossRefGoogle Scholar
13.Félix, Y. and Thomas, J.-C., The fibre-cofibre construction and its applications, J. Pure Appl. Algebra 53 (1988), 59–69.CrossRefGoogle Scholar
14.Félix, Y. and Thomas, J.-C., Effet d'un attachement cellulaire dans l'homologie de l'espace des lacets, Ann. Inst. Fourier 39 (1989), 207–224.CrossRefGoogle Scholar
15.Halperin, S. and Lemaire, J.-M., Suites inertes dans les algebres de Lie graduées (“Autopsie d'un meutre 2“), Math. Scand. 61 (1987), 39–67.CrossRefGoogle Scholar
16.Lemaire, J.-M., Algèbres connexes et homologie des espaces de lacets (Springer Lect. Notes Math 422, 1974).CrossRefGoogle Scholar
17.McCleary, J., On the mod p Betti numbers of loop spaces, Invent. Math. 87 (1987), 643–654.CrossRefGoogle Scholar
18.Milnor, J. W. and Moore, J. C., On the structure of Hopf algebras, Ann. of Math. (2) 81 (1965), 211–264.CrossRefGoogle Scholar
19.Moore, J. C., Differential Homological Algebra, in Proc. ICM 1970, I (Gauthier-Villars, Paris, 1971), 335–339.Google Scholar
20.Moore, J. C. and Smith, L., Hopf algebras and multiplicative fibrations I, Amer. J. Math. 90 (1968), 752–780.CrossRefGoogle Scholar