Article contents
The extraordinary higher tangent spaces of certain quadric intersections
Published online by Cambridge University Press: 20 January 2009
Abstract
Let Cr, be the intersection of n — r quadrics with a common self-polar simplex S in projective n-space [n]. Let Γr be a Cr that can be taken in coordinate form as 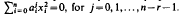 Every C1 is a Γ1, and its points of hyperosculation have special properties: they are the points of intersection of C1 with the faces of S each counting (n—1)(n — 2)/2 times, and the osculating [s], for s≦n–1, has 2s-point contact. Here we show that if r≧2 and n>2r then every point of Γ, has exceptional higher tangent spaces: the s-tangent space at a point P of an r-dimensional variety V is the intersection of all primes that cut V in a variety having an (s + l)-fold point (at least) at P, and normally has dimension
Every C1 is a Γ1, and its points of hyperosculation have special properties: they are the points of intersection of C1 with the faces of S each counting (n—1)(n — 2)/2 times, and the osculating [s], for s≦n–1, has 2s-point contact. Here we show that if r≧2 and n>2r then every point of Γ, has exceptional higher tangent spaces: the s-tangent space at a point P of an r-dimensional variety V is the intersection of all primes that cut V in a variety having an (s + l)-fold point (at least) at P, and normally has dimension 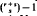 if this is less than n. The s-tangent space to Γ, at a point not in a face of S is an [rs] (provided rs <n). Usually it is the existence of lines on V through P that cause a lower than expected s-tangent dimension. Not so on Γr, since its lines form a subvariety. If n≧5 not every C2 is a Γ2. Take n≧5. We show that C2 is Γ2 if and only if C2 contains a line. Also C2 is a Γ2 if and only if at some one point of C2 off the faces of S the second-tangent space is a [4]. Thus, unexpectedly, we have: if one point of C2 off the faces of S has a [4] for second-tangent space, then so do all such points of C2. We obtain results for points of Γ, in the faces of S.
if this is less than n. The s-tangent space to Γ, at a point not in a face of S is an [rs] (provided rs <n). Usually it is the existence of lines on V through P that cause a lower than expected s-tangent dimension. Not so on Γr, since its lines form a subvariety. If n≧5 not every C2 is a Γ2. Take n≧5. We show that C2 is Γ2 if and only if C2 contains a line. Also C2 is a Γ2 if and only if at some one point of C2 off the faces of S the second-tangent space is a [4]. Thus, unexpectedly, we have: if one point of C2 off the faces of S has a [4] for second-tangent space, then so do all such points of C2. We obtain results for points of Γ, in the faces of S.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 3 , October 1992 , pp. 437 - 447
- Copyright
- Copyright © Edinburgh Mathematical Society 1992
References
REFERENCES
- 4
- Cited by


