No CrossRef data available.
Article contents
Extension of the “Medial Section” Problem (Euclid II :11, VI: 30, etc.) and derivation of a Hyperbolic Graph
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
To divide the straight line AB (containing a units) at C so that
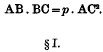
By algebra, taking the positive root,
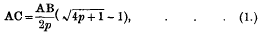
The number p may therefore have any positive value, integral or fractional, and when negative cannot exceed ¼. Secondly, AC and AB are incommensurable except when 4p +1 is a square:– e.g., if 4p = (q – l)(q +1) or if p = q(q+l), q being any positive integer or fraction.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1896
References
page 66 note * In the diagrams M is the mid-point of AB and in Figs. 1, 2, 3, SAK is LAB.


