Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
O'Regan, Donal
1996.
Resonant nonlinear singular problems in the limit circle case.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 3,
Issue. 1,
p.
55.
O’Regan, Donal
1997.
Existence Theory for Nonlinear Ordinary Differential Equations.
p.
105.
O’Regan, Donal
1997.
Existence Theory for Nonlinear Ordinary Differential Equations.
p.
116.
Asakawa, Hidekazu
2001.
Nonresonant singular two-point boundary value problems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 44,
Issue. 6,
p.
791.
El-Gebeily, Mohamed
and
O’Regan, Donal
2007.
A quasilinearization method for a class of second order singular nonlinear differential equations with nonlinear boundary conditions.
Nonlinear Analysis: Real World Applications,
Vol. 8,
Issue. 1,
p.
174.
El-Gebeily, Mohamed
and
O'Regan, Donal
2007.
Existence and boundary behavior for singular nonlinear differential equations with arbitrary boundary conditions.
Journal of Mathematical Analysis and Applications,
Vol. 334,
Issue. 1,
p.
140.
Jiang, Daqing
and
Zhang, Huina
2008.
Nonuniform nonresonant singular Dirichlet boundary value problems for the one-dimensional -Laplacian with sign changing nonlinearity.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 68,
Issue. 5,
p.
1155.
Pandey, R.K.
and
Verma, Amit K.
2010.
Monotone method for singular BVP in the presence of upper and lower solutions.
Applied Mathematics and Computation,
Vol. 215,
Issue. 11,
p.
3860.
Weng, Shiyou
Gao, Haiyin
Jiang, Daqing
and
Hou, Xuezhang
2011.
An existence principle for solutions to a singular boundary-value problems.
Journal of Mathematical Sciences,
Vol. 177,
Issue. 3,
p.
466.
Verma, Amit K.
Verma, Lajja
and
El-Gebeily, Mohamed A.
2011.
Nonlinear Singular BVP of Limit Circle Type and the Presence of Reverse‐Ordered Upper and Lower Solutions.
International Journal of Differential Equations,
Vol. 2011,
Issue. 1,
Fewster-Young, Nicholas
and
Tisdell, Christopher C.
2012.
The existence of solutions to second-order singular boundary value problems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 13,
p.
4798.
Verma, Amit K.
Pandit, Biswajit
Verma, Lajja
and
Agarwal, Ravi P.
2020.
A Review on a Class of Second Order Nonlinear Singular BVPs.
Mathematics,
Vol. 8,
Issue. 7,
p.
1045.
Chang, Shih-Hsiang
2024.
Regions of existence and uniqueness for singular two-point boundary value problems.
Mathematical Modelling and Analysis,
Vol. 29,
Issue. 4,
p.
753.


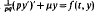 a.e. on [0, 1] with
a.e. on [0, 1] with 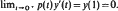 Here μ is such that
Here μ is such that 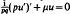 a.e. on [0, 1] with
a.e. on [0, 1] with 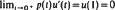 has only the trivial solution.
has only the trivial solution.