Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-03T19:16:16.958Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementary Proof that the Arithmetic Mean of any number of Positive Quantities is greater than the Geometric Mean*

Published online by Cambridge University Press:  20 January 2009

G. E. Crawford
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Def. The arithmetic mean of n quantities a, b, c, d …

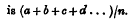
Def. The geometric mean of n quantities a, b, c, d …

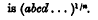
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 18 , February 1900 , pp. 2 - 4
Copyright
Copyright © Edinburgh Mathematical Society 1900

Footnotes

*

The above proof is a modification of the elegant proof given by Dr G. H. Bryan in his Middle Algebra, and was obviously suggested by it. No third proof on the same lines ean be given. Both have this logical advantage referred to by Dr Bryan, that the number of mental steps in the process is finite

References

* The above proof is a modification of the elegant proof given by Dr G. H. Bryan in his Middle Algebra, and was obviously suggested by it. No third proof on the same lines ean be given. Both have this logical advantage referred to by Dr Bryan, that the number of mental steps in the process is finite