Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T22:05:57.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamic asymptotic dimension for actions of virtually cyclic groups

Part of: Special aspects of infinite or finite groups Smooth dynamical systems: general theory Topological dynamics

Published online by Cambridge University Press:  04 May 2021

Massoud Amini ,
Kang Li ,
Damian Sawicki  and
Ali Shakibazadeh
Massoud Amini
Affiliation:
Department of Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran14115-134, Iran ([email protected])
Kang Li
Affiliation:
Institute of Mathematics of the Polish Academy of Sciences, Śniadeckich 8, Warsaw00-656, Poland ([email protected])
Damian Sawicki
Affiliation:
Max-Planck-Institut für Mathematik, Vivatsgasse 7, Bonn53111, Germany (guests.mpim-bonn.mpg.de/dsawicki/)
Ali Shakibazadeh
Affiliation:
Department of Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran14115-134, Iran ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the dynamic asymptotic dimension of an action of an infinite virtually cyclic group on a compact Hausdorff space is always one if the action has the marker property. This in particular covers a well-known result of Guentner, Willett, and Yu for minimal free actions of infinite cyclic groups. As a direct consequence, we substantially extend a famous result by Toms and Winter on the nuclear dimension of $C^{*}$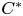-algebras arising from minimal free $\mathbb {Z}$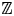-actions. Moreover, we also prove the marker property for all free actions of countable groups on finite-dimensional compact Hausdorff spaces, generalizing a result of Szabó in the metrisable setting.

Keywords

dynamic asymptotic dimensionmarker propertyminimal actionnuclear dimensionvirtually cyclic group

MSC classification

Primary: 37C45: Dimension theory of dynamical systems
Secondary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 20F69: Asymptotic properties of groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 364 - 372
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartels, A., Coarse flow spaces for relatively hyperbolic groups, Compos. Math. 153(4) (2017), 745–779.CrossRefGoogle Scholar
Bartels, A. and Lück, W., The Borel conjecture for hyperbolic and $\textrm {CAT}(0)$-groups, Ann. Math. 175(2) (2012), 631–689.CrossRefGoogle Scholar
Bartels, A., Lück, W. and Reich, H., Equivariant covers for hyperbolic groups, Geom. Topol. 12 (2008), 1799–1882.CrossRefGoogle Scholar
Deeley, R. J. and Strung, K. R., Nuclear dimension and classification of $\mathrm C^{*}$-algebras associated to Smale spaces, Trans. Am. Math. Soc. 370 (2018), 3467–3485.CrossRefGoogle Scholar
Dicks, W. and Dunwoody, M., Groups acting on graphs, Cambridge Studies in Advanced Mathematics, Volume 17 (Cambridge University Press, Cambridge, 1989).Google Scholar
Downarowicz, T., Minimal models for noninvertible and not uniquely ergodic systems, Israel J. Math. 156 (2006), 93–110.CrossRefGoogle Scholar
Farrell, F. T. and Jones, L. E., Isomorphism conjectures in algebraic K-theory, J. Am. Math. Soc. 6 (1993), 249–297.Google Scholar
Gromov, M., Asymptotic invariants of infinite groups, in Geometric group theory, Volume 2 (eds. G. Niblo and M. Roller), pp. vii+295 (London Mathematical Society, London, 1993).Google Scholar
Guentner, E., Willett, R. and Yu, G., Dynamical complexity and controlled operator $K$-theory, arXiv:1609.02093 [math.KT].Google Scholar
Guentner, E., Willett, R. and Yu, G., Dynamic asymptotic dimension: relation to dynamics, topology, coarse geometry, and $C^{*}$-algebras, Math. Ann. 367 (2017), 785–829.CrossRefGoogle Scholar
Gutman, Y., Mean dimension and Jaworski-type theorems, Proc. Lond. Math. Soc. 111 (2015), 831–850.CrossRefGoogle Scholar
Gutman, Y., Embedding topological dynamical systems with periodic points in cubical shifts, Ergodic Theory Dynam. Syst. 37(2) (2017), 512–538.CrossRefGoogle Scholar
Hirshberg, I. and Wu, J., The nuclear dimension of $C^{*}$-algebras associated to homeomorphisms, Adv. Math. 304 (2017), 56–89.CrossRefGoogle Scholar
Kerr, D., Dimension, comparison, and almost finiteness, J. Eur. Math. Soc. (JEMS) 22(11) (2020), 3697–3745.CrossRefGoogle Scholar
Putnam, I., The $C^{*}$-algebras associated with minimal homeomorphisms of the Cantor set, Pac. J. Math. 136(2) (1989), 329–353.CrossRefGoogle Scholar
Sawicki, D., Warped cones, (non-)rigidity, and piecewise properties. With a joint appendix with Dawid Kielak, Proc. Lond. Math. Soc. 118(4) (2019), 753–786.CrossRefGoogle Scholar
Szabó, G., The Rokhlin dimension of topological $\mathbb {Z}^{m}$-actions, Proc. Lond. Math. Soc. 110(3) (2015), 673–694.CrossRefGoogle Scholar
Szabó, G., Wu, J. and Zacharias, J., Rokhlin dimension for actions of residually finite groups, Ergodic Theory Dynam. Syst. 39(8) (2019), 2248–2304.CrossRefGoogle Scholar
Toms, A. S. and Winter, W., Minimal dynamics and K-theoretic rigidity: Elliott's conjecture, Geom. Funct. Anal. 23(1) (2013), 467–481.CrossRefGoogle Scholar
Winter, W. and Zacharias, J., The nuclear dimension of $C^{*}$-algebras, Adv. Math. 224(2) (2010), 461–498.CrossRefGoogle Scholar