The Differentiation of an Indefinite Integral

Extract

Theorem 1 needs very little explanation. It is the converse of the well known theorem that the indefinite integral F(x) of a function f(x) possesses a derivate on the right at every point at which f(x + 0) exists. If f(x + 0) does not exist, nothing can be said as to the existence or otherwise of F₊(x); but in a general way we might expect that the integral of a function which oscillates comparatively slowly, say sin (log x) at x = 0, would be more likely to possess a derivate than that of a function which oscillates more rapidly, say 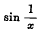. It appears from Theorem 1 that this is not by any means the case. In fact the integral of sin (log x) has not a definite derivate at x = 0 while that of 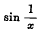has such a derivate.