Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Awami, M.
and
Thaheem, A. B.
1984.
A short proof of a decomposition theorem of a von Neumann algebra.
Proceedings of the American Mathematical Society,
Vol. 92,
Issue. 1,
p.
81.
Thaheem, A. B.
1987.
On certain decompositional properties of von Neumann algebras.
Glasgow Mathematical Journal,
Vol. 29,
Issue. 2,
p.
177.
THAHEEM, A.B.
1988.
Mathematical Analysis and its Applications.
p.
195.
Batty, C. J. K.
1989.
On certain pairs of automorphisms of C*-algebras.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 46,
Issue. 2,
p.
197.


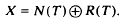
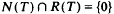 and, using dimension theory of finite dimensional spaces, that N(T) and R(T) span the whole space (see, for example, (2, pp. 271–73))
and, using dimension theory of finite dimensional spaces, that N(T) and R(T) span the whole space (see, for example, (2, pp. 271–73))