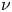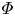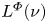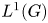Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Phonrakkhet, Sorravit
and
Wiboonton, Keng
2024.
Fourier Transform for $$L^p$$-Functions with a Vector Measure on a Homogeneous Space of Compact Groups.
Journal of Fourier Analysis and Applications,
Vol. 30,
Issue. 2,