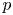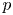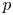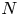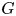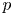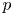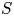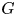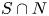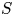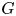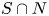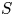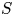Conjugacy conditions for supersoluble complements of an abelian base and a fixed point result for non-coprime actions

Abstract

We demonstrate that two supersoluble complements of an abelian base in a finite split extension are conjugate if and only if, for each prime $p$, a Sylow $p$-subgroup of one complement is conjugate to a Sylow $p$-subgroup of the other. As a corollary, we find that any two supersoluble complements of an abelian subgroup $N$ in a finite split extension $G$ are conjugate if and only if, for each prime $p$, there exists a Sylow $p$-subgroup $S$ of $G$ such that any two complements of $S\cap N$ in $S$ are conjugate in $G$. In particular, restricting to supersoluble groups allows us to ease D. G. Higman's stipulation that the complements of $S\cap N$ in $S$ be conjugate within $S$. We then consider group actions and obtain a fixed point result for non-coprime actions analogous to Glauberman's lemma.

1. Introduction

A finite group $G$ splits over a normal subgroup $N$ if there exists a complement $H$ such that $G\cong N\rtimes H$ forms a semidirect product. When $ |{N}|$ and $[G:N]$ are coprime, Schur proved a complement must exist and Zassenhaus demonstrated, under the additional assumption¹ that either $N$ or $G/N$ is soluble, that such a complement is unique up to conjugacy. When $N$ is abelian, Gaschütz showed a complement exists if and only if, for each prime $p$, there exists a Sylow $p$-subgroup $S$ of $G$ that splits over $S\cap N$. Higman considered the question of conjugacy for such complements and found that [2, cor. 2]

Corollary D. G. Higman

Let $G$ be a split extension of an abelian subgroup $N$. If for each prime $p$ there is a Sylow $p$-subgroup $S$ of $G$ such that any two complements of $S\cap N$ in $S$ are conjugate in $S$, then any two complements of $N$ in $G$ are conjugate.

In this note, we establish similar criteria for complements of an abelian base to be conjugate, loosening the restrictiveness of the conjugacy condition for the Sylow subgroups. To this end, we consider supersoluble groups, namely those groups $G$ that possess a series $1=G_0 \vartriangleleft G_1 \vartriangleleft \dotsb \vartriangleleft G_{s-1} \vartriangleleft G_s = G$ with each factor $G_i$ normal in $G$ and each quotient $G_{i+1}/G_i$ cyclic, for $0\leq i < s$. All finite nilpotent groups are supersoluble and in turn all supersoluble groups are soluble. We find that

Theorem 1 Suppose the supersoluble subgroups $H$ and $H'$ each complement a normal abelian subgroup $N$ in a finite group $G$. If for each prime $p$, $H'$ contains a conjugate of some Sylow $p$-subgroup of $H$, then $H$ and $H'$ are conjugate.

We then offer the following corollary, more in the spirit of Higman's work,

Corollary 1 Let $G$ be a split extension of an abelian subgroup $N$ such that $G/N$ is supersoluble. If for each prime $p$ there is a Sylow $p$-subgroup $S$ of $G$ such that any two complements of $S\cap N$ in $S$ are conjugate in $G$, then any two complements of $N$ in $G$ are conjugate.

If $G$ is supersoluble, then $G/N$ is as well. Thus, for supersoluble groups, complements of $S\cap N$ in $S$ need not be conjugated strictly within $S$ but merely in the full group $G$.

We then consider the fixed points of groups with operator groups, where Glauberman's result on the existence of fixed points for coprime actions [1, thm. 4] states

Lemma Glauberman

Given a finite group $H$ acting via automorphisms on a finite group $N$, suppose the induced semidirect product $N\rtimes H$ acts on some non-empty set $\varOmega$ where the action of $N$ is transitive. If the orders of $H$ and $N$ are coprime, then there exists an $H$-invariant element $\omega \in \varOmega$.

We offer an analogous fixed point result for non-coprime actions. In particular, Theorem 1 and Gaschütz's existence result allow us to demonstrate

Corollary 2 Given a finite supersoluble group $H$ acting via automorphisms on a finite abelian group $N,$ suppose the induced semidirect product $N\rtimes H$ acts on some non-empty set $\varOmega$ where the action of $N$ is transitive. If for each prime $p$, a Sylow $p$-subgroup of $H$ fixes some element of $\varOmega,$ then there exists an $H$-invariant element $\omega \in \varOmega$.

While Isaacs previously considered non-coprime actions and outlined some conditions for the existence of a fixed point [3], results of this nature appear to be rare in the literature.

1.1. Outline

We proceed as follows. In the remainder of this section, we introduce some notation before proving the main theorem in § 2. We then prove the corollaries in § 3 and make concluding remarks in § 4.

1.2. Notation

All groups in this note are assumed to be finite. We use standard notation readily found in any introductory textbook on group theory, such as Isaacs’ [4]. We let groups act from the left and denote conjugation by $g^\gamma = \gamma ^{-1}g\gamma$ for $g,\,\gamma \in G$. For subgroups $J$ and $K$ of $G$, we let $N_K(J)$ and $C_K(J)$ denote the elements of $K$ that normalize and centralize $J$, respectively. In the semidirect product $G \cong N \rtimes H$, we note that any two complements of $N$ are necessarily isomorphic (to the quotient group $G/N$) and that $N_K(J) = C_K(J)$ whenever both $K\leq N$ and $J \leq H$, as then $[J,\, N_K(J)] \leq J \cap N = 1$.

2. Proof of main theorem

We first restrict $N$ to be an abelian $p$-subgroup and then consider the general case that $N$ is abelian. In both cases that follow, we assume we are given supersoluble complements $H$ and $H'$ of a nontrivial subgroup $N\vartriangleleft G$ satisfying the hypotheses of Theorem 1. The theorem would hold trivially if $H$ were a $q$-subgroup for some prime $q$, so without loss, at least two distinct primes divide $|{H}|$. Zassenhaus's result further implies $p$ must be one of these primes. As any two Sylow subgroups of $H$ are conjugate within $H$ for a given prime, our assumptions imply that $H'$ contains some conjugate of every Sylow subgroup of $H$ where each such conjugate is itself a Sylow subgroup of $H'$. Furthermore, as any element $g\in G$ can be uniquely written $g=hn$ for some $n\in N$ and $h\in H$, we may assume that for each prime $p$, there exists a Sylow $p$-subgroup $P$ of $H$ such that $P^n\leq H'$ for some $n\in N$.

2.1. Case that $N$ is a $p$-subgroup

We first suppose $N$ is a $p$-subgroup for some prime $p$ and induct on the order of $G$. As $H$ is supersoluble, we may find a normal subgroup $H_0 \vartriangleleft H$ of index $q$ [4, exer. 3B.9], where $q$ is the smallest prime divisor of $|{H}|$. Under the inductive hypothesis, $H_0$ is conjugate to some subgroup of $H'$ and so the left action of $H_0$ on the cosets $\varOmega =G/H'$ has a fixed point, say $n'H'$. If $H$ itself does not fix any point of $\varOmega$, then the non-empty set $\operatorname {Fix}_{\varOmega }(H_0)$ of points in $\varOmega$ fixed by $H_0$ may be partitioned into orbits of $H$, each having cardinality $[H:H_0] = q$. On the other hand, the map from $N_N(H_0)$ to $\operatorname {Fix}_{\varOmega }(H_0)$ given by $n\mapsto n\cdot n'H'$ provides a bijective correspondence between these two sets, and as $N_N(H_0) \leq N$ is a $p$-group, we may assume without loss that $q=p$. In particular, $H_0$ contains a $p'$-Hall subgroup of $H$, say $M$, such that $C_N(M) \supseteq C_N(H_0) = N_N(H_0)$ is nontrivial. Furthermore, we may assume without loss that $M\vartriangleleft H$ [4, exer. 3B.8] so $N_0 := [N,\, M] \vartriangleleft G$ where $N=N_0 \times C_N(M)$ by a theorem of Fitting [4, thm. 4.34]. Consequently, $N_0$ is a strict subgroup of $N$.

Let $P$ be a Sylow $p$-subgroup of $H$. By hypothesis, there exists some $n \in N$ such that $P^n \leq H'$. Replacing $H$ by $H^n$ in the statement of the theorem if necessary, we may assume without loss that $n$ is trivial, i.e. that $P \leq H'$.

Glauberman's lemma implies the left action of $NM/N_0$ on the cosets $G/N_0H'$ has an $M$-invariant element. As $N=N_0 \times C_N(M)$, it follows that $\overline {N} = \overline {C_N(M)}$ in $\overline G = G/N_0$. Furthermore, as fixed points come from fixed points in coprime actions [4, cor. 3.28], $\overline {N} = C_{\overline N}(M)$ so that $M$ fixes every element of $G/N_0 H'$. In particular, $M\leq N_0H'$ so that $N_0M$ acts on the cosets $N_0H'/H'$. Glauberman's lemma implies this second action also has an $M$-invariant element so that $M^{n_0} \leq H'$ for some $n_0 \in N_0$. Thus, as $H\leq N_0H'$, we may apply the inductive hypothesis in $N_0H'$ to conclude that $H$ and $H'$ are conjugate.

2.2. General case that $N$ is abelian

We again induct on the order of $G$. Building upon the results of our first case, we now assume $|{N}|$ has multiple prime divisors. In particular, we may write $N=N_1\times N_2$ where $N_1$ and $N_2$ are characteristic in $N$ and thus normal in $G$. (We may, for example, let $N_1$ be the first primary component of $N$ and $N_2$ be the product of the other primary components.) In $G/N_1$, the inductive hypothesis implies the action of $H$ on the left cosets $G/N_1H'$ has a fixed point, say $n_2N_1H'$ for some $n_2\in N_2$. Analogously, in $G/N_2$, we find that the action of $H$ on $G/N_2H'$ must also have a fixed point, say $n_1N_2H'$ for some $n_1\in N_1$. Consequently, we conclude that the action of $H$ on $G/H'$ fixes $n_1n_2H'$ so that $H$ and $H'$ are conjugate.

3. Proofs of corollaries

In this section, we provide proofs for the corollaries stated in § 1.

3.1. Proof of Corollary 1

Given a group $G$ satisfying the hypotheses of Corollary 1, we suppose by way of contradiction that $H$ and $H'$ complement $N$ in $G$ but fail to be conjugate. By Theorem 1, there exists a prime $p$ and Sylow $p$-subgroups $P$ and $P'$ of $H$ and $H'$, respectively, such that $P$ and $P'$ fail to be conjugate in $G$. Let $L$ be the unique Sylow $p$-subgroup of $N$. Then $LP$ and $LP'$ are Sylow $p$-subgroups of $G$ and thus are conjugate to the Sylow $p$-subgroup $S$ of $G$ specified in the statement of the corollary. In particular, $LP^{g_1}=L(P')^{g_2}=S$ for some $g_1,\,g_2\in G$ where $S\cap N = L$, so that by assumption, $P^{g_1}$ and $({P'})^{g_2}$ are conjugate in $G$, a contradiction.

3.2. Proof of Corollary 2

Suppose $G=N \rtimes H$ acts on a set $\varOmega$ according to the hypotheses of Corollary 2. Fix some $\alpha \in \varOmega$ and consider the point stabilizer $G_\alpha$ of $\alpha$ in $G$. As $N$ is transitive on $\varOmega$, for any $g\in G$, we have $g\cdot \alpha = n\cdot \alpha$ for some $n\in N$, so that $n^{-1}g \in G_\alpha$. Thus, $G=NG_\alpha$. As $N\vartriangleleft G$, it follows that $G_\alpha \cap N \vartriangleleft G_\alpha$.

We claim $G_\alpha$ splits over $G_\alpha \cap N$. By Gaschütz's theorem, it suffices to show that for each prime $p$, there exists a Sylow p-subgroup S of $G_\alpha$ that splits over $S\cap N$. Fix $p$, an arbitrary prime. By hypothesis, there exists some $n\in N$ and a Sylow $p$-subgroup $P$ of $H$ such that $P^n \leq G_\alpha$. Let $L$ be the Sylow $p$-subgroup of $G_\alpha \cap N$. As ${|{G_\alpha }| = |{G_\alpha \cap N}| [G:N]}$, it follows that $S=LP^n$ is a Sylow subgroup of $G_\alpha$ and $P^n$ is a complement of $S \cap N = L$ in that subgroup.

Thus, $G_\alpha$ splits and we may let $H'$ complement $G_\alpha \cap N$ in $G_\alpha$. It follows that $|{H'}| = [G_\alpha : G_\alpha \cap N] = [G:N]$ so $H'$ complements $N$ in $G$. Theorem 1 then implies that ${H'=H^n}$ for some $n\in N$ so that $H$ fixes $n \cdot \alpha$.

4. Concluding remarks

We conclude with some historical context.

4.1. Conjugacy of complements

D. G. Higman's work included another result on the conjugacy of complements that we mention here for completeness. In a split extension $G\cong N\rtimes H$ of an abelian subgroup $N$, Higman considered an intermediate subgroup $N\leq B \leq G$ of index $[G:B]=b$ such that the map $n\mapsto n^b$ for $n\in N$ has an inverse. (Such an inverse always exists if $b$ and $|{N}|$ are coprime, for example.) He showed that if any two complements of $N$ in $B$ are conjugate in $B$, then any two complements of $N$ in $G$ are conjugate in $G$. Furthermore, given two specific complements $H$ and $H'$ of $N$ in $G$, he showed that $H$ and $H'$ are conjugate in $G$ if and only if $H\cap B$ and $H'\cap B$ are conjugate in $B$ [2, cor. 1].

4.2. Fixed points

Glauberman's original paper [1] provided two conditions for $N$-transitive actions of split extensions $G\cong N\rtimes H$ that jointly imply the existence of an $H$-invariant element, namely (S) if $W\leq G$ satisfies $WN=G$ then $W$ splits over $W\cap N$, and (Z) any two complements of $N$ in $G$ are conjugate.² The hypotheses of our Corollary 2 do not necessarily imply (Z) but rather only that two specific complements of $N$ are conjugate, namely $H$ and a complement of $G_\alpha$ in $G_\alpha \cap N$, where $\alpha \in \varOmega$ is a member of the set on which $G$ acts. For this reason, we did not directly apply Glauberman's result but instead mirrored his proof.

To further illustrate the connection between the conjugacy of complements and the fixed points of certain group actions, we note that Corollary 2 implies Theorem 1. To see this equivalence, we may apply Corollary 2 to the action of $N\rtimes H$ on the set $\varOmega =G/H'$ of left cosets for any second complement $H'$ satisfying the hypotheses of Theorem 1.

Finally, we note that in the language of group cohomology, Corollary 1 provides a vanishing condition for the first cohomology group $H^1(H,\,N)$ of the split extension $G\cong N\rtimes H$ when $N$ is abelian and $H$ is supersoluble.