Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-01T03:49:38.114Z Has data issue: false hasContentIssue false
  • English
  • Français

A configuration of lines in three dimensions

Published online by Cambridge University Press:  20 January 2009

J. W. P. Hirschfeld
J. W. P. Hirschfeld
Affiliation:
University of Sussex, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1849, Cayley and Salmon discovered that a general cubic surface in projective space of three dimensions over the complex numbers has twenty-seven lines on it. They remarked that all the properties of the twenty-seven lines would not become apparent until a better notation than they had given was found. This notation was discovered by Schläfli in 1858 in the double-six theorem (henceforth referred to as 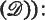given five skew linesa1, …, a5with a single transversal b6such that no four of the ai lie in a regulus, the four ai excluding aj have a second transversal bj and the five lines b1, …, b5thus obtained have a transversal a6—the completing line of the double-six. The other fifteen lines of the cubic surface are then 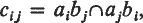, where ai bj is the plane containing ai and bj.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 18 , Issue 2 , December 1972 , pp. 105 - 123
Copyright
Copyright © Edinburgh Mathematical Society 1972

References

REFERENCES

(1) Baker, H. F., Principles of Geometry, Vol. III (Cambridge University Press, 1923).Google Scholar
(2) Bourbaki, N., Groupes et Alg`bres de Lie, Ch. 4, 5, and 6 (Hermann, Paris, 1968).Google Scholar
(3) Brown, L. M., A configuration of points and spheres in four-dimensional space, Proc. Roy. Soc. Edinburgh Sect. A 64 (1955), 145–149.Google Scholar
(4) Coxeter, H. S. M., Math. Reviews 17 (1956), 886.Google Scholar
(5) Coxeter, H. S. M., Regular Polytopes (Macmillan, 1963).Google Scholar
(6) Grace, J. H., Circles, spheres and linear complexes, Trans. Cambridge Philos. Soc. 16 (1898), 153–190.Google Scholar
(7) Hirschfeld, J. W. P., Classical configurations over finite fields: I. The double-six and the cubic surface with 27 lines, Rend. Mat. e Appl. 26 (1967), 115–152.Google Scholar
(8) Hirschfeld, J. W. P., Classical configurations over finite fields: II. Grace's extension of the double-six, Rend. Mat. e Appl. 26 (1967), 349–374.Google Scholar
(9) Hirschfeld, J. W. P., A projective configuration, Computational Problems in Abstract Algebra (Pergamon, 1970), 321–324.Google Scholar
(10) Kubota, T., On double sixers, Sci. Rep. Tôhuku Univ. 6 (1917), 89–94.Google Scholar
(11) Longuet-Higgins, M. S., A numerical disproof of a conjecture in projective geometry, Proc. Roy. Soc. Ser. A 323 (1971), 443–453.Google Scholar
(12) Salmon, G., Higher Plane Curves (3rd ed., Dublin, 1879).Google Scholar
(13) Todd, J. A., Configurations defined by six lines in space of three dimensions, Proc. Cambridge Phitos. Soc. 29 (1933), 52–68.CrossRefGoogle Scholar
(14) Wren, T. L., Some applications of the two-three birational space transformation. Proc. London Math. Soc. 15 (1916), 144–165.Google Scholar