Article contents
A completeness theorem for a nonlinear problem
Published online by Cambridge University Press: 20 January 2009
Extract
As is well known, the linear Sturm-Liouville eigenvalue problem on a bounded real interval [a, b] possesses a family of eigenfunctions which is a complete orthonormal system for the real Hilbert space L2[a, b], i.e. there exists a sequence of eigenfunctions un such that (ui, uj) = δij (Kronecker delta) for i, j ∈ N (the set of positive integers) and, if u ∈ L2[a, b], u = 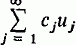 where cj = (u, uj). Pimbley (4, p. 113), raises the question as to whether similar completeness results hold for nonlinear problems. In this note we show that certain nonlinear Sturm-Liouville eigenvalue problems possess eigenfunctions which form a basis for L2[a, b], i.e. there exists a sequence of eigenfunctions {vn} for the nonlinear problem such that every u ∈ L2[a, b] can be expressed in the form u =
where cj = (u, uj). Pimbley (4, p. 113), raises the question as to whether similar completeness results hold for nonlinear problems. In this note we show that certain nonlinear Sturm-Liouville eigenvalue problems possess eigenfunctions which form a basis for L2[a, b], i.e. there exists a sequence of eigenfunctions {vn} for the nonlinear problem such that every u ∈ L2[a, b] can be expressed in the form u = 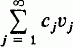 by means of a unique sequence {cn} of real numbers.
by means of a unique sequence {cn} of real numbers.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 2 , September 1974 , pp. 169 - 172
- Copyright
- Copyright © Edinburgh Mathematical Society 1974
References
REFERENCES
- 3
- Cited by


