Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T21:35:03.855Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactness of Commutators of One-Sided Singular Integrals in Weighted Lebesgue Spaces

Part of: Inequalities Harmonic analysis in several variables

Published online by Cambridge University Press:  10 January 2019

Víctor García García  and
Pedro Ortega Salvador
Víctor García García
Affiliation:
Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071, Málaga, Spain ([email protected]; [email protected])
Pedro Ortega Salvador
Affiliation:
Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071, Málaga, Spain ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that if p > 1, 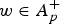$w\in A_p^ +$, b ∈ CMO and $C_b^ + $ is the commutator with symbol b of a Calderón–Zygmund convolution singular integral with kernel supported on (−∞, 0), then 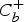$C_b^ + $ is compact from Lp(w) into itself.

Keywords

commutatorscompact operatorscompactnessweights

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory
Secondary: 26D10: Inequalities involving derivatives and differential and integral operators
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 3 , August 2019 , pp. 655 - 665
Copyright
Copyright © Edinburgh Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Aimar, H., Forzani, L. and Martín-Reyes, F. J., On weighted inequalities for singular integrals, Proc. Amer. Math. Soc. 125(7) (1997), 2057–2064.Google Scholar
2.Benyi, A., Damian, W., Moen, K. and Torres, R., Compact bilinear commutators: the weighted case, Michigan Math. J. 64(1) (2015), 39–51.Google Scholar
3.Calderón, A., Commutators of singular integral operators, Proc. Natl. Acad. Sci. USA 53 (1965), 1092–1099.Google Scholar
4.Clop, A. and Cruz, V., Weighted estimates for Beltrami equations, Ann. Acad. Sci. Fenn. Math. 38 (2013), 91–113.Google Scholar
5.Coifman, R. and Fefferman, C., Weighted norm inequalities for maximal functions and singular integrals, Stud. Math. 51 (1974), 241–250.Google Scholar
6.Coifman, R., Rochberg, R. and Weiss, G., Factorization theorems for Hardy spaces in several variables, Ann. Math. 103(2) (1976), 611–635.Google Scholar
7.Krantz, S. G. and Li, S., Boundedness and compactness of integral operators on spaces of homogeneous type and applications, II, J. Math. Anal. Appl. 258 (2001), 642–657.Google Scholar
8.Lorente, M. and Riveros, M. S., Weighted inequalities for commutators of one-sided singular integrals, Comment. Math. Univ. Carolin. 43(1) (2002), 83–101.Google Scholar
9.Martín-Reyes, F. J., Ortega Salvador, P. and de la Torre, A., Weighted inequalities for one-sided maximal functions, Trans. Amer. Math. Soc. 319 (1990), 517–534.Google Scholar
10.Muckenhoupt, B., Weighted norm inequalities for the Hardy maximal function, Trans. Amer. Math. Soc. 165 (1972), 207–226.Google Scholar
11.Ortega, P., Weighted inequalities for one-sided maximal functions in Orlicz spaces, Stud. Math. 131(2) (1998), 101–114.Google Scholar
12.Pérez, C., Sharp estimates for commutators of singular integrals via iterations of the Hardy–Littlewood maximal function, J. Fourier Anal. Appl. 3(6) (1997), 743–756.Google Scholar
13.Sawyer, E., Weighted inequalities for the one-sided Hardy–Littlewood maximal functions, Trans. Amer. Math. Soc. 297 (1986), 53–61.Google Scholar
14.Uchiyama, A., On the compactness of operators of Hankel type, Tohoku Math. J. 30 (1978), 163–171.Google Scholar
15.Yosida, K., Functional analysis, Classics in Mathematics, Volume 6 (Springer-Verlag, Berlin, 1995).Google Scholar