Article contents
Commuting well-bounded operators on Hilbert spaces
Published online by Cambridge University Press: 20 January 2009
Extract
A bounded linear operator T on a complex reflexive Banach space is said to be well-bounded if it is possible to choose a compact interval J = [a, b] and a positive constant M such that
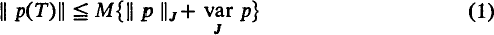
for every complex polynomial p, where ‖p‖J denotes sup {|p(t)|:t ∈ J}. Such operators were introduced and first studied by Smart (4). They are of interest principally because they admit (and in fact are characterised by) an integral representation similar to, but in general weaker than, the integral representation of a self-adjoint operator on a Hilbert space. (See (2) and (4) for details.) It is easily seen, by verifying (1) directly, that T is well-bounded if it is a scalar-type spectral operator with real spectrum.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 20 , Issue 2 , September 1976 , pp. 167 - 172
- Copyright
- Copyright © Edinburgh Mathematical Society 1976
References
REFERENCES
- 2
- Cited by


