No CrossRef data available.
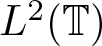 $L^2(\mathbb{T})$
$L^2(\mathbb{T})$Published online by Cambridge University Press: 11 January 2024
Consider the multiplication operator MB in 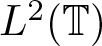 $L^2(\mathbb{T})$, where the symbol B is a finite Blaschke product. In this article, we characterize the commutant of MB in
$L^2(\mathbb{T})$, where the symbol B is a finite Blaschke product. In this article, we characterize the commutant of MB in 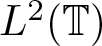 $L^2(\mathbb{T})$. As an application of this characterization result, we explicitly determine the class of conjugations commuting with
$L^2(\mathbb{T})$. As an application of this characterization result, we explicitly determine the class of conjugations commuting with 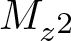 $M_{z^2}$ or making
$M_{z^2}$ or making 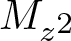 $M_{z^2}$ complex symmetric by introducing a new class of conjugations in
$M_{z^2}$ complex symmetric by introducing a new class of conjugations in 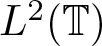 $L^2(\mathbb{T})$. Moreover, we analyse their properties while keeping the whole Hardy space, model space and Beurling-type subspaces invariant. Furthermore, we extended our study concerning conjugations in the case of finite Blaschke products.
$L^2(\mathbb{T})$. Moreover, we analyse their properties while keeping the whole Hardy space, model space and Beurling-type subspaces invariant. Furthermore, we extended our study concerning conjugations in the case of finite Blaschke products.