No CrossRef data available.
Article contents
Cohomology of induced modules in rings of differential operators
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let K be a field of characteristic zero and let Δ ={δ1,…,δn} be a set of commuting K-derivations of the commutative Noetherian K-algebra R. Let S = R[X1,…,Xn] be the corresponding ring of differential operators, so [Xi, r] = Xir − rXi=δi(r and [Xi, Xj]=0, for 1≦i, j≦n. Let M be a maximal ideal of R with R/M of finite dimension over K. The purpose of this note is to describe the groups
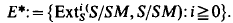
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 31 , Issue 1 , February 1988 , pp. 41 - 47
- Copyright
- Copyright © Edinburgh Mathematical Society 1988
References
REFERENCES
3.Goodearl, K. and Lenegan, T. H., Krull dimension of differential operator rings IV—multiple derivations, Proc. London Math. Soc. (3) 47 (1983), 306–336.CrossRefGoogle Scholar
4.Lipman, J., Free derivation modules on algebraic varieties, Amer. J. Math. 87 (1965), 874–898.CrossRefGoogle Scholar
5.Rotman, J., An Introduction to Homological Algebra (Academic Press, New York, 1979).Google Scholar
6.Zariski, O. and Samuel, P., Commutative Algebra, Volume II (Van Nostrand, Princeton, 1960).CrossRefGoogle Scholar


