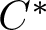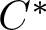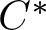1. Introduction
Thedynamics of ![]() ${C^*}$-algebras has long been an area of interest for operator algebraists, and crossed product duality provides an important tool in this study. This crossed product theory simplifies when acting groups are abelian, but the wide array of uses left a desire for generalizations to duality suitable for non-abelian groups. A significant achievement of this desire was furnished by the duality theorem of Imai and Takai, which depended on the design of coactions to replace the role of the dual group in the non-abelian setting. While these objects greatly generalized dynamical results, the cost was significant. The loss of the dual group in favour of coactions in this setting cast this new field into a challenging intersection of tensor products and multiplier algebras.
${C^*}$-algebras has long been an area of interest for operator algebraists, and crossed product duality provides an important tool in this study. This crossed product theory simplifies when acting groups are abelian, but the wide array of uses left a desire for generalizations to duality suitable for non-abelian groups. A significant achievement of this desire was furnished by the duality theorem of Imai and Takai, which depended on the design of coactions to replace the role of the dual group in the non-abelian setting. While these objects greatly generalized dynamical results, the cost was significant. The loss of the dual group in favour of coactions in this setting cast this new field into a challenging intersection of tensor products and multiplier algebras.
Independently, the introduction of graph algebras in the late twentieth century shed much new light in the field of operator algebras. Popularized as ![]() ${C^*}$-algebras that you can ‘see’, graph algebras succinctly relate the algebraic structure of the
${C^*}$-algebras that you can ‘see’, graph algebras succinctly relate the algebraic structure of the ![]() ${C^*}$-algebra to observable combinatorial data associated to the defining (directed) graph. Their ongoing study is simultaneously tractable and fruitful, since on one hand the hope of using simple pictures to analyse a
${C^*}$-algebra to observable combinatorial data associated to the defining (directed) graph. Their ongoing study is simultaneously tractable and fruitful, since on one hand the hope of using simple pictures to analyse a ![]() ${C^*}$-algebra is both clear and stimulating, while on the other hand
${C^*}$-algebra is both clear and stimulating, while on the other hand ![]() ${C^*}$-algebras from across the field have found natural expressions as graph algebras. Once again, this wide array of uses has produced an interest in generalizing the constructions of graph algebras, which have been pursued along many different lines. Examples include higher ranked graphs, Exel-Laca algebras, topological graphs and the subject of this paper, topological quivers.
${C^*}$-algebras from across the field have found natural expressions as graph algebras. Once again, this wide array of uses has produced an interest in generalizing the constructions of graph algebras, which have been pursued along many different lines. Examples include higher ranked graphs, Exel-Laca algebras, topological graphs and the subject of this paper, topological quivers.
One boon graph algebras offered to the theory of non-abelian duality is the incredible leverage offered by ‘seeing’ how the coactions work in the context of graph algebras. The first result of this type [Reference Kaliszewski, Quigg and Raeburn11] considered labellings of the edge set by a discrete group, introducing a new directed graph whose vertex and edge sets are products of the originals with the discrete group. At the same time, this labelling induced a coaction on the original graph algebra, and the authors showed in [Reference Kaliszewski, Quigg and Raeburn11, Theorem 2.4] that these two constructions are isomorphic using the technology devoted to graph algebras, namely Cuntz-Krieger families and the Gauge-Invariant Uniqueness Theorem.
Later, Katsura codified the data of a graph algebra into a ![]() ${C^*}$-correspondence [Reference Katsura15] and offered the modern perspective [Reference Katsura14] that the graph algebra of a specified graph is the universal
${C^*}$-correspondence [Reference Katsura15] and offered the modern perspective [Reference Katsura14] that the graph algebra of a specified graph is the universal ![]() ${C^*}$-algebra for (what we would call today) Cuntz–Pimsner covariant homomorphisms of the associated
${C^*}$-algebra for (what we would call today) Cuntz–Pimsner covariant homomorphisms of the associated ![]() ${C^*}$-correspondence. Here, universal means that every Cuntz–Pimsner covariant representation of the correspondence into a
${C^*}$-correspondence. Here, universal means that every Cuntz–Pimsner covariant representation of the correspondence into a ![]() ${C^*}$-algebra induces a homomorphism from the universal algebra into the representing algebra. Simultaneously, Katsura introduced the notion of topological graphs, which offered the first continuous analog to directed graphs by applying topological constraints on the data.
${C^*}$-algebra induces a homomorphism from the universal algebra into the representing algebra. Simultaneously, Katsura introduced the notion of topological graphs, which offered the first continuous analog to directed graphs by applying topological constraints on the data.
Equipped with the technology of Cuntz–Pimsner covariant homomorphisms into ![]() ${C^*}$-algebras, Kaliszewski, Quigg and Robertson introduced the notion of Cuntz–Pimsner covariance for morphisms between correspondences [Reference Kaliszewski, Quigg and Robertson12]. There, they showed that the passage from
${C^*}$-algebras, Kaliszewski, Quigg and Robertson introduced the notion of Cuntz–Pimsner covariance for morphisms between correspondences [Reference Kaliszewski, Quigg and Robertson12]. There, they showed that the passage from ![]() ${C^*}$-correspondences to the Cuntz–Pimsner algebra was functorial between a suitable pair of categories. Shortly after, these three authors investigated this functor for correspondences equipped with a coaction [Reference Kaliszewski, Quigg and Robertson13], deducing that a suitable correspondence coaction generates a coaction on the associated Cuntz–Pimsner algebra. Kaliszewski and Quigg then used this machinery to recover for Katsura’s topological graphs what had been discovered for directed graphs [Reference Kaliszewski and Quigg10]. The skew product topological graph by a (locally compact) group is isomorphic to the crossed product by a naturally occurring coaction, producing this time a coaction that you can ‘see’ in the continuous setting.
${C^*}$-correspondences to the Cuntz–Pimsner algebra was functorial between a suitable pair of categories. Shortly after, these three authors investigated this functor for correspondences equipped with a coaction [Reference Kaliszewski, Quigg and Robertson13], deducing that a suitable correspondence coaction generates a coaction on the associated Cuntz–Pimsner algebra. Kaliszewski and Quigg then used this machinery to recover for Katsura’s topological graphs what had been discovered for directed graphs [Reference Kaliszewski and Quigg10]. The skew product topological graph by a (locally compact) group is isomorphic to the crossed product by a naturally occurring coaction, producing this time a coaction that you can ‘see’ in the continuous setting.
Around the time that Katsura studied his topological graphs, Muhly and Solel introduced topological quivers to exemplify traits in the study of Morita equivalence of tensor algebras. Muhly and Tomforde later took up the task of investigating the associated ![]() ${C^*}$-algebras in [Reference Muhly and Tomforde16]. Apart from the matter of convention (and we conform to the conventions of Katsura here), the principle difference between quivers and topological graphs is that topological graphs insist that the source map is a local homeomorphism, while quivers insist only that the source map is open. To make up for this freedom, we insist that the fibres over any vertex can be appropriately measured, and the authors follow the strategy used for measuring groupoids by a system of measures. In this article, we take up the study of skew products for topological quivers.
${C^*}$-algebras in [Reference Muhly and Tomforde16]. Apart from the matter of convention (and we conform to the conventions of Katsura here), the principle difference between quivers and topological graphs is that topological graphs insist that the source map is a local homeomorphism, while quivers insist only that the source map is open. To make up for this freedom, we insist that the fibres over any vertex can be appropriately measured, and the authors follow the strategy used for measuring groupoids by a system of measures. In this article, we take up the study of skew products for topological quivers.
In § 2, we record our conventions for bundles, topological quivers and associated constructions, and coactions. Starting with § 3, we introduce the skew product quiver and produce a Gross–Tucker type classification for skew products. In § 4, we study the associated ![]() ${C^*}$-algebras in earnest, culminating in the main objective Theorem 4.3. We end with a section on applications, where we offer an open problem regarding qualities of the coaction and show that the reduced crossed product by the dual action is Morita equivalent to the
${C^*}$-algebras in earnest, culminating in the main objective Theorem 4.3. We end with a section on applications, where we offer an open problem regarding qualities of the coaction and show that the reduced crossed product by the dual action is Morita equivalent to the ![]() ${C^*}$-algebra of the original quiver.
${C^*}$-algebra of the original quiver.
2. Preliminaries
2.1 Bundle constructions
In the development of bundles, we follow [Reference Husemoller9], but we define principal bundles according to the hypothesis of [Reference Raeburn and Williams20, Lemma 4.63]. The remark following the cited lemma reconciles the disparity in definitions.
Definition 2.1. A bundle is a triple ![]() $(E, p, B)$, where
$(E, p, B)$, where ![]() $p:E\to B$ is a continuous function.
$p:E\to B$ is a continuous function. ![]() $B$ is called the base space,
$B$ is called the base space, ![]() $E$ the total space,
$E$ the total space, ![]() $p$ the bundle projection, and for each
$p$ the bundle projection, and for each ![]() $b\in B$, the space
$b\in B$, the space ![]() $p^{-1}(b)$ is called the fibre over
$p^{-1}(b)$ is called the fibre over ![]() $b$. We often identify a bundle with its bundle projection.
$b$. We often identify a bundle with its bundle projection.
A bundle morphism is a pair of continuous maps ![]() $(u, f): (E, p, B)\to (E', p', B')$ with
$(u, f): (E, p, B)\to (E', p', B')$ with ![]() $p'u=fp$, i.e. the diagram below commutes.
$p'u=fp$, i.e. the diagram below commutes.

A bundle isomorphism is an invertible bundle morphism (which requires each map ![]() $u, f$ to be a homeomorphism).
$u, f$ to be a homeomorphism).
Example 2.2. Given a bundle ![]() $(E, p, B)$ and a continuous map
$(E, p, B)$ and a continuous map ![]() $f: C \to B$, the space
$f: C \to B$, the space
is called the pullback under f, and the triple ![]() $(E*_f C, \text{pr}_2, C)$ is a bundle, where
$(E*_f C, \text{pr}_2, C)$ is a bundle, where ![]() $\text{pr}_2$ is the standard projection onto the second factor. The pair
$\text{pr}_2$ is the standard projection onto the second factor. The pair ![]() $(\text{pr}_2, f)$ is then a bundle morphism.
$(\text{pr}_2, f)$ is then a bundle morphism.
Example 2.3. A topological group ![]() $G$ acts on the right a locally compact Hausdorff space
$G$ acts on the right a locally compact Hausdorff space ![]() $X$ provided there is a continuous group anti-homomorphism
$X$ provided there is a continuous group anti-homomorphism ![]() $\alpha:G\to \text{Homeo}(X)$ (written
$\alpha:G\to \text{Homeo}(X)$ (written ![]() $\alpha(g)(x)=xg$), and we call such a space a right
$\alpha(g)(x)=xg$), and we call such a space a right ![]() $G$-space.
$G$-space. ![]() $G$ acts freely on
$G$ acts freely on ![]() $X$ provided all stabilizers are trivial.
$X$ provided all stabilizers are trivial. ![]() $G$ acts properly on
$G$ acts properly on ![]() $X$ if the translation map
$X$ if the translation map ![]() $(x, g)\mapsto (x, xg)$ is a proper map. The action is called principal if
$(x, g)\mapsto (x, xg)$ is a proper map. The action is called principal if ![]() $G$ acts both freely and properly. If
$G$ acts both freely and properly. If ![]() $G$ acts on the right of
$G$ acts on the right of ![]() $X$, then the triple
$X$, then the triple ![]() $(X, q, X/ G)$ is a bundle, where
$(X, q, X/ G)$ is a bundle, where ![]() $X/ G$ (the set of orbits of G) is given the quotient topology induced by the quotient map
$X/ G$ (the set of orbits of G) is given the quotient topology induced by the quotient map ![]() $q$. This is called the quotient bundle for the
$q$. This is called the quotient bundle for the ![]() $G$ action. When
$G$ action. When ![]() $G$ acts principally on
$G$ acts principally on ![]() $X$, then the space
$X$, then the space ![]() $X/ G$ is also locally compact and Hausdorff.
$X/ G$ is also locally compact and Hausdorff.
For ![]() $g\in G$, the pair
$g\in G$, the pair ![]() $(\text{rt}_g, \text{id})$ is a bundle morphism of
$(\text{rt}_g, \text{id})$ is a bundle morphism of ![]() $q$, where
$q$, where ![]() $\text{rt}_g(x) = xg$ is right translation by
$\text{rt}_g(x) = xg$ is right translation by ![]() $g$, and this morphism is invertible.
$g$, and this morphism is invertible.
Definition 2.4 Given a locally compact group ![]() $G$, a bundle
$G$, a bundle ![]() $p$ is a
$p$ is a ![]() $G$-bundle provided the total space
$G$-bundle provided the total space ![]() $E$ is a
$E$ is a ![]() $G$-space and there is a bundle isomorphism
$G$-space and there is a bundle isomorphism ![]() $(\text{id},f): (E, p, B)\to (E, q, E/ G)$. A
$(\text{id},f): (E, p, B)\to (E, q, E/ G)$. A ![]() $G$-bundle
$G$-bundle ![]() $p$ is called principal if
$p$ is called principal if ![]() $G$ acts freely and properly on the total space. In this case, the fibre
$G$ acts freely and properly on the total space. In this case, the fibre ![]() $p^{-1}(b)$ over any point is isomorphic to
$p^{-1}(b)$ over any point is isomorphic to ![]() $G$.
$G$.
A ![]() $G$-bundle morphism is a bundle morphism
$G$-bundle morphism is a bundle morphism ![]() $(u, f):(E, p, B)\to (E', p', B')$ whose map of total spaces is equivariant for the
$(u, f):(E, p, B)\to (E', p', B')$ whose map of total spaces is equivariant for the ![]() $G$-action, that is
$G$-action, that is ![]() $u(xg) = u(x)g$.
$u(xg) = u(x)g$.
Example 2.5. If ![]() $(E, p, B)$ is a
$(E, p, B)$ is a ![]() $G$-bundle and
$G$-bundle and ![]() $f:C\to B$ is continuous, then there is a
$f:C\to B$ is continuous, then there is a ![]() $G$-action on
$G$-action on ![]() $C*_f E$ given by
$C*_f E$ given by ![]() $(c, e)g = (c, eg)$ making the pullback into a
$(c, e)g = (c, eg)$ making the pullback into a ![]() $G$-bundle over
$G$-bundle over ![]() $C$. The pullback bundle inherits any structure enjoyed by the original bundle.
$C$. The pullback bundle inherits any structure enjoyed by the original bundle.
The following theorem will be foundational for us. For details, see [Reference Husemoller9, Theorem 4.4.2] and the discussion surrounding [Reference Palais18, Proposition 1.3.4]. This result also holds for groupoids, see [Reference Hall, Kaliszewski, Quigg and Williams7] and the references therein.
Theorem 2.6. Suppose we have principal G-bundles ![]() $p:E\to B$ and
$p:E\to B$ and ![]() $p':E'\to B'$, together with a
$p':E'\to B'$, together with a ![]() $G$-bundle morphism
$G$-bundle morphism ![]() $(u, f):(E, p, B)\to (E', p', B')$. Then the assignment
$(u, f):(E, p, B)\to (E', p', B')$. Then the assignment
 \begin{align*}
E&\to B*_f E'\\
e&\mapsto (p(e), u(e))
\end{align*}
\begin{align*}
E&\to B*_f E'\\
e&\mapsto (p(e), u(e))
\end{align*} is a ![]() $G$-equivariant homeomorphism between
$G$-equivariant homeomorphism between ![]() $E'$ and
$E'$ and ![]() $B*_f E'$. In particular, this map produces a
$B*_f E'$. In particular, this map produces a ![]() $G$-bundle isomorphism from
$G$-bundle isomorphism from ![]() $E$ to
$E$ to ![]() $B*_f E'$ over
$B*_f E'$ over ![]() $B$.
$B$.
Definition 2.7 ([Reference Williams21], § 3.2)
Given a bundle ![]() $\pi: E\to B$, a system of measures over
$\pi: E\to B$, a system of measures over ![]() $\pi$, or
$\pi$, or ![]() $\pi$-system, is a family of positive Radon measures
$\pi$-system, is a family of positive Radon measures ![]() $\lambda = \{\lambda_b: b\in B\}$ defined on E and satisfying two conditions
$\lambda = \{\lambda_b: b\in B\}$ defined on E and satisfying two conditions
(1) the support of
 $\lambda_b$ is a subset of the fibre over
$\lambda_b$ is a subset of the fibre over  $b$ and
$b$ and(2) for any
 $f\in C_c(E)$, the assignment
$f\in C_c(E)$, the assignment
 \begin{equation*}b\mapsto \lambda(f)(b) := \int f \,\mathrm{d}\lambda_b\end{equation*}
\begin{equation*}b\mapsto \lambda(f)(b) := \int f \,\mathrm{d}\lambda_b\end{equation*}is a continuous function.
Condition 2 is called continuity for the system. A ![]() $\pi$-system is called full provided
$\pi$-system is called full provided ![]() $\text{supp}(\lambda_b) = \pi^{-1}(b)$, and proper provided
$\text{supp}(\lambda_b) = \pi^{-1}(b)$, and proper provided ![]() $\lambda_b\neq 0$ for every
$\lambda_b\neq 0$ for every ![]() $b\in B$. We will confine our attention to full and proper
$b\in B$. We will confine our attention to full and proper ![]() $\pi$-systems.
$\pi$-systems.
Suppose the spaces ![]() $E, B$ admit (right) actions by a group
$E, B$ admit (right) actions by a group ![]() $G$ and
$G$ and ![]() $\pi$ is equivariant for the action. A
$\pi$ is equivariant for the action. A ![]() $\pi$-system is called equivariant provided
$\pi$-system is called equivariant provided
 \begin{equation*}\int_E f(eg)\,\mathrm{d}\lambda_b(e) = \int_E f(e)\,\mathrm{d}\lambda_{bg}(e)\end{equation*}
\begin{equation*}\int_E f(eg)\,\mathrm{d}\lambda_b(e) = \int_E f(e)\,\mathrm{d}\lambda_{bg}(e)\end{equation*} for every ![]() $f\in C_c(E)$,
$f\in C_c(E)$, ![]() $b\in B$, and
$b\in B$, and ![]() $g\in G$.
$g\in G$.
If ![]() $G$ acts principally on each of
$G$ acts principally on each of ![]() $E, B$ and if
$E, B$ and if ![]() $\pi$ is equivariant and surjective, then there is a canonical map
$\pi$ is equivariant and surjective, then there is a canonical map ![]() $\dot{\pi}$ making the diagram
$\dot{\pi}$ making the diagram

commute. The orbit map for ![]() $E$ induces a homeomorphism
$E$ induces a homeomorphism ![]() $\pi^{-1}(b)\to \dot{\pi}^{-1}(bG)$, so that equivariance of
$\pi^{-1}(b)\to \dot{\pi}^{-1}(bG)$, so that equivariance of ![]() $\lambda$ induces for each orbit
$\lambda$ induces for each orbit ![]() $bG\in B\backslash G$ a measure
$bG\in B\backslash G$ a measure ![]() $\mu_{bG}$ with support
$\mu_{bG}$ with support ![]() $\dot{\pi}(bG)$. For
$\dot{\pi}(bG)$. For ![]() $\phi\in C_c(E\backslash G)$, this measure is given by
$\phi\in C_c(E\backslash G)$, this measure is given by
 \begin{equation*}\int \phi \,\mathrm{d}\mu_{bG}.\end{equation*}
\begin{equation*}\int \phi \,\mathrm{d}\mu_{bG}.\end{equation*} In this circumstance, we have the following theorem relating ![]() $G$-equivariant
$G$-equivariant ![]() $\pi$-systems to those of their orbits.
$\pi$-systems to those of their orbits.
Theorem 2.8 ([Reference Williams21], Proposition 3.14)
Let ![]() $G$ be a group,
$G$ be a group, ![]() $E$ and
$E$ and ![]() $B$ principal right
$B$ principal right ![]() $G$-spaces, and
$G$-spaces, and ![]() $\pi: E\to B$ a continuous open surjection. Let
$\pi: E\to B$ a continuous open surjection. Let ![]() $\dot{\pi}$ be the induced map for the orbit spaces of
$\dot{\pi}$ be the induced map for the orbit spaces of ![]() $E$ and
$E$ and ![]() $B$.
$B$.
(a) If
 $\lambda$ is an invariant
$\lambda$ is an invariant  $\pi$-system, then the induced family of measures
$\pi$-system, then the induced family of measures  $\mu=\{\mu_{bG}\}_{bG\in B\backslash G}$ is a
$\mu=\{\mu_{bG}\}_{bG\in B\backslash G}$ is a  $\dot{\pi}$-system.
$\dot{\pi}$-system.(b) If
 $\mu$ is a
$\mu$ is a  $\dot\pi$-system, then there is a
$\dot\pi$-system, then there is a  $\pi$-system
$\pi$-system  $\lambda$ whose induced
$\lambda$ whose induced  $\dot\pi$-system agrees with
$\dot\pi$-system agrees with  $\mu$.
$\mu$.
2.2.  ${C^*}$-Constructions for topological quivers
${C^*}$-Constructions for topological quivers
We refer to [Reference Muhly and Tomforde16] for topological quivers but adapt the definitions to the conventions of [Reference Katsura15, Reference Raeburn19], which we use along with [Reference Echterhoff, Kaliszewski, Quigg and Raeburn5].
Definition 2.9. A topological quiver is an ensemble ![]() $\mathcal{Q}=\{E^0,E^1, r, s, \lambda\}$ comprising the following data:
$\mathcal{Q}=\{E^0,E^1, r, s, \lambda\}$ comprising the following data:
•
 $E^1$ and
$E^1$ and  $E^0$ are locally compact Hausdorff spaces.
$E^0$ are locally compact Hausdorff spaces.•
 $r$ and
$r$ and  $s$ are continuous from
$s$ are continuous from  $E^1$ to
$E^1$ to  $E^0$.
$E^0$.•
 $s$ is open.
$s$ is open.•
 $\lambda$ is a full
$\lambda$ is a full  $s$-system
$s$-system
Remark 2.10. ![]() $r$ and
$r$ and ![]() $s$ are called the range map and source map, elements of
$s$ are called the range map and source map, elements of ![]() $E^1$ are typically called edges and elements of
$E^1$ are typically called edges and elements of ![]() $E^0$ vertices. These names are anticipated by the analogy of quivers with directed graphs [Reference Raeburn19], which are essentially quivers whose edge and vertex spaces are discrete and countable, and the family
$E^0$ vertices. These names are anticipated by the analogy of quivers with directed graphs [Reference Raeburn19], which are essentially quivers whose edge and vertex spaces are discrete and countable, and the family ![]() $\lambda$ (typically suppressed in this context) consists of counting measures. A vertex which is in the image of the source map but not the range map is called a source, and a vertex which is in the image of the range map but not the source map is called a sink. Using the technique of adding tails to quivers (cf. [Reference Muhly and Tomforde16, § 4]), one can always restrict their attention to quivers without sinks. We will often briefly call a topological quiver a quiver.
$\lambda$ (typically suppressed in this context) consists of counting measures. A vertex which is in the image of the source map but not the range map is called a source, and a vertex which is in the image of the range map but not the source map is called a sink. Using the technique of adding tails to quivers (cf. [Reference Muhly and Tomforde16, § 4]), one can always restrict their attention to quivers without sinks. We will often briefly call a topological quiver a quiver.
Given a topological quiver ![]() $\mathcal{Q}$, [Reference Muhly and Tomforde16] defines a quiver
$\mathcal{Q}$, [Reference Muhly and Tomforde16] defines a quiver ![]() $C^*$-correspondence as follows: Let
$C^*$-correspondence as follows: Let ![]() $A=C_0(E^0)$. For
$A=C_0(E^0)$. For ![]() $X_0=C_c(E^1)$, there is an A-valued inner product
$X_0=C_c(E^1)$, there is an A-valued inner product ![]() $\langle\cdot,\cdot\rangle:X_0\times X_0\to A$ by
$\langle\cdot,\cdot\rangle:X_0\times X_0\to A$ by
 \begin{equation*}\langle\eta,\xi\rangle(v) = \int \overline{\eta(e)}\xi(e)\,\mathrm{d}\lambda_v(e).\end{equation*}
\begin{equation*}\langle\eta,\xi\rangle(v) = \int \overline{\eta(e)}\xi(e)\,\mathrm{d}\lambda_v(e).\end{equation*} We then get left and right actions of ![]() $f\in A$ on
$f\in A$ on ![]() $\xi \in X_0$ by
$\xi \in X_0$ by
 \begin{align*}
f\xi(e) &= f(r(e))\xi(e) \text{ and}\\
\xi f(e) &= \xi(e)f(s(e)),
\end{align*}
\begin{align*}
f\xi(e) &= f(r(e))\xi(e) \text{ and}\\
\xi f(e) &= \xi(e)f(s(e)),
\end{align*} which encode in the module ![]() $X_0$ the structure of the topological quiver. Denoting by
$X_0$ the structure of the topological quiver. Denoting by ![]() $X$ the completion of
$X$ the completion of ![]() $X_0$ with respect to this inner product,
$X_0$ with respect to this inner product, ![]() $X$ is an
$X$ is an ![]() $A-A$ correspondence. In fact, for
$A-A$ correspondence. In fact, for ![]() $A'=C_0(E^1)$,
$A'=C_0(E^1)$, ![]() $X$ is also an
$X$ is also an ![]() $A'-A$ correspondence with the left action given by pointwise multiplication. Notice that, whether we regard
$A'-A$ correspondence with the left action given by pointwise multiplication. Notice that, whether we regard ![]() $X$ as an
$X$ as an ![]() $A-A$ correspondence or an
$A-A$ correspondence or an ![]() $A'-A$ correspondence,
$A'-A$ correspondence, ![]() $X$ is non-degenerate, by which we mean that
$X$ is non-degenerate, by which we mean that ![]() $\overline{\text{span}}(A\cdot X) = \overline{\text{span}}(A'\cdot X) = X$. In fact, the Cohen–Hewitt Factorization Theorem guarantees that
$\overline{\text{span}}(A\cdot X) = \overline{\text{span}}(A'\cdot X) = X$. In fact, the Cohen–Hewitt Factorization Theorem guarantees that ![]() $A\cdot X= X$, so authors will often take this to be the definition of non-degeneracy for
$A\cdot X= X$, so authors will often take this to be the definition of non-degeneracy for ![]() ${C^*}$-correspondences.
${C^*}$-correspondences.
Remark 2.11 When we declare a left action of a ![]() ${C^*}$-algebra
${C^*}$-algebra ![]() $A$ on
$A$ on ![]() $X$, what we really mean is a homomorphism
$X$, what we really mean is a homomorphism ![]() $\phi_A: A\to \mathcal{L}(X)$. In particular, that the left action of
$\phi_A: A\to \mathcal{L}(X)$. In particular, that the left action of ![]() $A'$ on
$A'$ on ![]() $X$ is implemented by pointwise multiplication, and the left action by
$X$ is implemented by pointwise multiplication, and the left action by ![]() $A$ is induced by the range map by assigning
$A$ is induced by the range map by assigning ![]() $f\mapsto f\circ r$ and then acting by pointwise multiplication. In our context, this homomorphism ϕA is faithful when the set of sources has empty interior.
$f\mapsto f\circ r$ and then acting by pointwise multiplication. In our context, this homomorphism ϕA is faithful when the set of sources has empty interior.
Given the ![]() ${C^*}$-correspondence of a topological quiver, we are interested in constructing a
${C^*}$-correspondence of a topological quiver, we are interested in constructing a ![]() ${C^*}$-algebra which reflects the quiver’s data. We will also find value in representing the correspondence of one quiver in the correspondence of another quiver in a way which preserves the ‘essential’ structure of interest to us. In what follows, recall that for an
${C^*}$-algebra which reflects the quiver’s data. We will also find value in representing the correspondence of one quiver in the correspondence of another quiver in a way which preserves the ‘essential’ structure of interest to us. In what follows, recall that for an ![]() $A-A$ correspondence
$A-A$ correspondence ![]() $X$, the multiplier correspondence is
$X$, the multiplier correspondence is ![]() $M(X)=\mathcal{L}_A(A,X),$ the space of all adjointable
$M(X)=\mathcal{L}_A(A,X),$ the space of all adjointable ![]() $A$-linear operators from
$A$-linear operators from ![]() $A$ (regarded as the standard correspondence over itself) into
$A$ (regarded as the standard correspondence over itself) into ![]() $X$.
$X$. ![]() $M(X)$ is an
$M(X)$ is an ![]() $M(A)-M(A)$ correspondence. Given a pair
$M(A)-M(A)$ correspondence. Given a pair ![]() $(X, A), (Y, B)$ of correspondences, a morphism of correspondences is a pair
$(X, A), (Y, B)$ of correspondences, a morphism of correspondences is a pair ![]() $(\psi, \pi):(X, A)\to (M(Y),M(B))$ of maps consisting of a homomorphism
$(\psi, \pi):(X, A)\to (M(Y),M(B))$ of maps consisting of a homomorphism ![]() $\pi:A\to M(B)$ and a linear map
$\pi:A\to M(B)$ and a linear map ![]() $\psi:X\to M(Y)$ which preserves the correspondence operations. A representation of
$\psi:X\to M(Y)$ which preserves the correspondence operations. A representation of ![]() $(X,A)$ in a
$(X,A)$ in a ![]() ${C^*}$-algebra
${C^*}$-algebra ![]() $D$ is a correspondence homomorphism
$D$ is a correspondence homomorphism ![]() $(\psi, \pi):(X,A)\to (M(D), M(D))$ into the multiplier of the standard correspondence associated to
$(\psi, \pi):(X,A)\to (M(D), M(D))$ into the multiplier of the standard correspondence associated to ![]() $D$. We are interested in a particular class of correspondence homomorphisms.
$D$. We are interested in a particular class of correspondence homomorphisms.
Definition 2.12. ([Reference Kaliszewski, Quigg and Robertson12], Definition 3.1)
A correspondence homomorphism is Cuntz–Pimsner covariant provided
(i)
 $\psi(X)\subset M_B(Y) = \{y\in M(Y): B\cdot y\cup y\cdot B\subset Y\}$
$\psi(X)\subset M_B(Y) = \{y\in M(Y): B\cdot y\cup y\cdot B\subset Y\}$(ii)
 $\pi:A\to M(B)$ is non-degenerate
$\pi:A\to M(B)$ is non-degenerate(iii)
 $\pi(J_X)\subset M(B; J_Y)$
$\pi(J_X)\subset M(B; J_Y)$(iv) The following diagram commutes

Remark 2.13. Above, ![]() $J_X$ is the largest ideal mapping
$J_X$ is the largest ideal mapping ![]() $A$ injectively into
$A$ injectively into ![]() $\mathbb{K}(X)$ (likewise for
$\mathbb{K}(X)$ (likewise for ![]() $J_Y$),
$J_Y$), ![]() $\psi^{(1)}$ is the naturally occurring map from
$\psi^{(1)}$ is the naturally occurring map from ![]() $\mathbb{K}(X)$ to
$\mathbb{K}(X)$ to ![]() $M(\mathbb{K}(Y))$, and
$M(\mathbb{K}(Y))$, and
For topological quivers, [Reference Muhly and Tomforde16, Proposition 3.15] provides a satisfactory description of ![]() $J_X$ in terms of the regular vertices of the topological quiver, themselves defined in [Reference Muhly and Tomforde16, Definition 3.14]. The regular vertices are characterized as
$J_X$ in terms of the regular vertices of the topological quiver, themselves defined in [Reference Muhly and Tomforde16, Definition 3.14]. The regular vertices are characterized as
 \begin{equation*}
E^0_{\text{reg}}=E^0_{\text{fin}}\cap \text{Int}(\overline{r(E^1)}),
\end{equation*}
\begin{equation*}
E^0_{\text{reg}}=E^0_{\text{fin}}\cap \text{Int}(\overline{r(E^1)}),
\end{equation*}where
 \begin{align*}
E^0_{\text{fin}} = \{v\in E^0 : \text{there exists a precompact neighbourhood $V$ of $v$ such that } r^{-1}(\overline{V}) \\
\text{is compact and } s|_{r^{-1}(V)} \text{ is a local homeomorphism}\}.\
\end{align*}
\begin{align*}
E^0_{\text{fin}} = \{v\in E^0 : \text{there exists a precompact neighbourhood $V$ of $v$ such that } r^{-1}(\overline{V}) \\
\text{is compact and } s|_{r^{-1}(V)} \text{ is a local homeomorphism}\}.\
\end{align*} According to Definition 2.12, [Reference Kaliszewski, Quigg and Robertson12, Theorem 3.7] defines a functor from the category of ![]() ${C^*}$-correspondences with Cuntz–Pimsner covariant homomorphisms to the category of
${C^*}$-correspondences with Cuntz–Pimsner covariant homomorphisms to the category of ![]() ${C^*}$-algebras with non-degenerate homomorphisms. Through the remainder of this article, we denote by
${C^*}$-algebras with non-degenerate homomorphisms. Through the remainder of this article, we denote by ![]() $(X,A)$ the
$(X,A)$ the ![]() $A-A$ correspondence associated to
$A-A$ correspondence associated to ![]() $\mathcal{Q}$ and
$\mathcal{Q}$ and ![]() $(C^*(\mathcal{Q}), k_X, k_A)$ the universal Cuntz–Pimsner covariant representation of
$(C^*(\mathcal{Q}), k_X, k_A)$ the universal Cuntz–Pimsner covariant representation of ![]() $(X,A)$. This universal
$(X,A)$. This universal ![]() ${C^*}$-algebra is the definition of the
${C^*}$-algebra is the definition of the ![]() ${C^*}$-algebra associated with
${C^*}$-algebra associated with ![]() $\mathcal{Q}$.
$\mathcal{Q}$.
2.3. Coaction constructions
For a detailed exposition on coactions, one can consult the appendix to [Reference Echterhoff, Kaliszewski, Quigg and Raeburn5]. Antecedents for this article are due to [Reference Kaliszewski, Quigg and Robertson13].
Definition 2.14. Given a locally compact group ![]() $G$ and a
$G$ and a ![]() ${C^*}$-algebra
${C^*}$-algebra ![]() $A$, a coaction
$A$, a coaction ![]() $(A,\delta)$ of
$(A,\delta)$ of ![]() $G$ is an injective non-degenerate homomorphism
$G$ is an injective non-degenerate homomorphism
which satisfies the coassociative condition,
together with coaction non-degeneracy
Remark 2.15. The theory of coactions makes emphatic use of the group ![]() ${C^*}$-algebra together with tensor products, and these structures are deeply bound to the theory. Consider, for example, that for a locally compact group
${C^*}$-algebra together with tensor products, and these structures are deeply bound to the theory. Consider, for example, that for a locally compact group ![]() $G$, we can associate with the canonical homomorphism
$G$, we can associate with the canonical homomorphism ![]() $\iota: G\hookrightarrow M(C^* (G))$ a distinguished unitary
$\iota: G\hookrightarrow M(C^* (G))$ a distinguished unitary ![]() $w_G\in UM(C_0(G)\otimes C^* (G))$ as follows. We identify
$w_G\in UM(C_0(G)\otimes C^* (G))$ as follows. We identify ![]() $M(C_0(G)\otimes C^* (G))$ with
$M(C_0(G)\otimes C^* (G))$ with ![]() $C_b(G, M^\beta(C^* (G) ))$, the bounded continuous functions from
$C_b(G, M^\beta(C^* (G) ))$, the bounded continuous functions from ![]() $G$ into
$G$ into ![]() $M(C^* (G) )$ endowed with the strict topology, and then define
$M(C^* (G) )$ endowed with the strict topology, and then define ![]() $\omega_G$ by
$\omega_G$ by ![]() $w_G(g)=\iota(g)\in M(C^* (G) )$. This unitary casts the embedding
$w_G(g)=\iota(g)\in M(C^* (G) )$. This unitary casts the embedding ![]() $\iota$ into the theory of tensor products, which allows us to describe covariant representations of coactions in the following discussion.
$\iota$ into the theory of tensor products, which allows us to describe covariant representations of coactions in the following discussion.
One special example of a coaction is implemented by a homomorphism ![]() $\psi:C_0(G)\to M(A)$, according to the assignment
$\psi:C_0(G)\to M(A)$, according to the assignment
 \begin{align*}
\delta^\psi:A&\to M(A\otimes C^* (G) )\\
a&\mapsto \text{Ad}(\psi\otimes\text{id}(w_G))(a\otimes 1)\\
\end{align*}
\begin{align*}
\delta^\psi:A&\to M(A\otimes C^* (G) )\\
a&\mapsto \text{Ad}(\psi\otimes\text{id}(w_G))(a\otimes 1)\\
\end{align*} and such a coaction is termed inner. Much as in the theory of actions, we define a covariant representation of ![]() $(A, \delta)$ as a pair of non-degenerate homomorphisms
$(A, \delta)$ as a pair of non-degenerate homomorphisms ![]() $(\pi, \mu)$ such that the diagram
$(\pi, \mu)$ such that the diagram

commutes. Loosely speaking, a covariant representation provides a setting where the coaction ![]() $\delta$ acts as an inner coaction.
$\delta$ acts as an inner coaction.
Remark 2.16. In the full generality of locally compact groups, it is necessary for us to work with multiplier algebras frequently. The use of multiplier algebras affords us the power to consider strict extensions of homomorphisms, which under non-degeneracy conditions are unique. There are natural questions about the compatibility of strict extensions under composition, which in practice cause us no concern. Consequently, by abuse of notation, we commonly will identify a homomorphism with its strict extension. One can follow [Reference Huef, Quigg, Raeburn and Williams8, appendix] for more details on the general theory.
Definition 2.17. A crossed product for a coaction is a ![]() ${C^*}$-algebra
${C^*}$-algebra ![]() $A\rtimes_\delta G$ together with a covariant representation
$A\rtimes_\delta G$ together with a covariant representation ![]() $(j_A, j_G): (A,\delta)\to M(A\rtimes_\delta G)$ that is universal for covariant representations. That is, if
$(j_A, j_G): (A,\delta)\to M(A\rtimes_\delta G)$ that is universal for covariant representations. That is, if ![]() $(\pi, \mu): (A,\delta)\to M(B)$ is any covariant representation of the coaction, there is a unique non-degenerate homomorphism
$(\pi, \mu): (A,\delta)\to M(B)$ is any covariant representation of the coaction, there is a unique non-degenerate homomorphism ![]() $\pi\times\mu: A\rtimes_\delta G\to M(B)$ with the property that
$\pi\times\mu: A\rtimes_\delta G\to M(B)$ with the property that
 \begin{align*}
\pi=(\pi\times\mu)\circ j_A\\
\mu=(\pi\times\mu)\circ j_G.\\
\end{align*}
\begin{align*}
\pi=(\pi\times\mu)\circ j_A\\
\mu=(\pi\times\mu)\circ j_G.\\
\end{align*} ![]() $\pi\times \mu$ is called the integrated form of the representation
$\pi\times \mu$ is called the integrated form of the representation ![]() $(\pi, \mu)$.
$(\pi, \mu)$.
Remark 2.18. Let ![]() $(A, \delta, G)$ be a coaction and consider the multiplication representation
$(A, \delta, G)$ be a coaction and consider the multiplication representation ![]() $M:C_0(G)\to M(\mathbb{K}(L^2 (G) ))$. Then one covariant representation for
$M:C_0(G)\to M(\mathbb{K}(L^2 (G) ))$. Then one covariant representation for ![]() $(A,\delta)$ is implemented by the pair
$(A,\delta)$ is implemented by the pair
which is called the regular representation of the coaction. The integrated form of this representation is always faithful, indicating a departure from the theory of actions on ![]() ${C^*}$-algebras. Instead, the notion of ‘intermediate’ completions for
${C^*}$-algebras. Instead, the notion of ‘intermediate’ completions for ![]() ${C^*}$-dynamical systems is recovered in this dual category by different classes of coactions. We will shortly introduce the two most important classes.
${C^*}$-dynamical systems is recovered in this dual category by different classes of coactions. We will shortly introduce the two most important classes.
Fix ![]() $s\in G$. Another example of a representation for
$s\in G$. Another example of a representation for ![]() $(A,\delta)$ is given by the pair
$(A,\delta)$ is given by the pair ![]() $(j_A, j_G\circ \text{rt}_s):(A,\delta)\to M(A\times_\delta G)$, which determines an automorphism of
$(j_A, j_G\circ \text{rt}_s):(A,\delta)\to M(A\times_\delta G)$, which determines an automorphism of ![]() $A\times_\delta G$. The family of integrated forms indexed by the elements of G produces an action of G on the crossed product, called the dual action to
$A\times_\delta G$. The family of integrated forms indexed by the elements of G produces an action of G on the crossed product, called the dual action to ![]() $\delta$, and denoted by
$\delta$, and denoted by ![]() $\hat\delta$.
$\hat\delta$.
Definition 2.19 (cf. [Reference Huef, Quigg, Raeburn and Williams8], [Reference Echterhoff, Kaliszewski and Quigg4])
A coaction ![]() $(A,\delta)$ is called normal provided the canonical homomorphism
$(A,\delta)$ is called normal provided the canonical homomorphism ![]() $j_A:A\to M (A\times_\delta G )$ is faithful.
$j_A:A\to M (A\times_\delta G )$ is faithful.
A coaction ![]() $(A, \delta)$ is called maximal provided there is an isomorphism
$(A, \delta)$ is called maximal provided there is an isomorphism
 \begin{equation*}
A\times_\delta G\times_{\hat{\delta}} G \cong A\otimes \mathbb{K}(L^2(G))
\end{equation*}
\begin{equation*}
A\times_\delta G\times_{\hat{\delta}} G \cong A\otimes \mathbb{K}(L^2(G))
\end{equation*}given by a certain canonical map.
A given coaction ![]() $(A,\delta)$ always has both a normalization
$(A,\delta)$ always has both a normalization ![]() $(A^n,\delta^n)$ and a maximalization
$(A^n,\delta^n)$ and a maximalization ![]() $(A^m, \delta^m)$, and there are natural surjections
$(A^m, \delta^m)$, and there are natural surjections ![]() $A\to A^n$ and
$A\to A^n$ and ![]() $A^m\to A$. It is possible for a coaction to be both maximal and normal. This has strong implications for the dual action, as we see below.
$A^m\to A$. It is possible for a coaction to be both maximal and normal. This has strong implications for the dual action, as we see below.
Proposition 2.20. Suppose ![]() $(A, \delta)$ is a coaction. δ is both normal and maximal if and only if the dual action
$(A, \delta)$ is a coaction. δ is both normal and maximal if and only if the dual action ![]() $\hat{\delta}$ is amenable in the sense that the regular representation
$\hat{\delta}$ is amenable in the sense that the regular representation
 \begin{equation*}A\times_\delta G\times_{\hat{\delta}} G \to A\times_\delta G\times_{\hat{\delta}, r} G\end{equation*}
\begin{equation*}A\times_\delta G\times_{\hat{\delta}} G \to A\times_\delta G\times_{\hat{\delta}, r} G\end{equation*}is an isomorphism.
Proof. This is an immediate consequence of [Reference Echterhoff, Kaliszewski and Quigg4, Proposition 2.2], which the authors illustrate pictorially with the commutative diagram

In the diagram, ![]() $\Lambda$ is the regular representation for the crossed product,
$\Lambda$ is the regular representation for the crossed product, ![]() $\Phi$ is the canonical surjection, and ψ is the quotient map
$\Phi$ is the canonical surjection, and ψ is the quotient map ![]() $\psi:A\to A/\ker{j_A}$ associated to the universal map
$\psi:A\to A/\ker{j_A}$ associated to the universal map ![]() $j_A:A\to A\times_\delta G$. Their proof furnishes the isomorphism
$j_A:A\to A\times_\delta G$. Their proof furnishes the isomorphism ![]() $\Upsilon$ and the surjection
$\Upsilon$ and the surjection ![]() $\Psi$.
$\Psi$.
For the forward direction, see that since ![]() $\delta$ is a maximal coaction, the map
$\delta$ is a maximal coaction, the map ![]() $\Phi$ is injective, and since
$\Phi$ is injective, and since ![]() $\delta$ is normal,
$\delta$ is normal, ![]() $\ker{j_A}=\{0\}$ and
$\ker{j_A}=\{0\}$ and ![]() $\psi$ is the identity. It now follows that
$\psi$ is the identity. It now follows that
a composition of isomorphisms.
For the reverse implication, notice that ![]() $\Lambda = \Psi\circ \Phi$, so since
$\Lambda = \Psi\circ \Phi$, so since ![]() $\Lambda$ is injective and
$\Lambda$ is injective and ![]() $\Phi$ is always surjective,
$\Phi$ is always surjective, ![]() $\Phi$ is an isomorphism.
$\Phi$ is an isomorphism. ![]() $\Phi$ is the canonical map for
$\Phi$ is the canonical map for ![]() $A\times_\delta G\times_{\hat \delta} G\to A\otimes \mathbb{K}(L^2(G))$, so that
$A\times_\delta G\times_{\hat \delta} G\to A\otimes \mathbb{K}(L^2(G))$, so that ![]() $\delta$ is maximal. Pursuing normality, consider
$\delta$ is maximal. Pursuing normality, consider
is an isomorphism, so that in particular ![]() $\psi:A\to A/\ker{j_A}$ is injective. Thus,
$\psi:A\to A/\ker{j_A}$ is injective. Thus, ![]() $\ker{j_A} = \{0\}$, and
$\ker{j_A} = \{0\}$, and ![]() $\delta$ is normal.
$\delta$ is normal.
Finally, we will make use of the notion of coactions for ![]() ${C^*}$-correspondences. The relevant definition is supplied below.
${C^*}$-correspondences. The relevant definition is supplied below.
Definition 2.21. Let ![]() $X$ be an
$X$ be an ![]() $A-B$ correspondence,
$A-B$ correspondence, ![]() $G$ a locally compact group and
$G$ a locally compact group and ![]() $\delta, \epsilon$ coactions of
$\delta, \epsilon$ coactions of ![]() $G$ on
$G$ on ![]() $A$ and
$A$ and ![]() $B$ respectively. A coaction of
$B$ respectively. A coaction of ![]() $G$ on
$G$ on ![]() $X$ is a non-degenerate correspondence homomorphism
$X$ is a non-degenerate correspondence homomorphism
which has ![]() $\delta$ and
$\delta$ and ![]() $\epsilon$ as coefficient maps, and such that
$\epsilon$ as coefficient maps, and such that
(i)
 $\overline{\text{span}}((1_{M(A)}\otimes C^*(G))\sigma(X)) = X\otimes C^*(G)$
$\overline{\text{span}}((1_{M(A)}\otimes C^*(G))\sigma(X)) = X\otimes C^*(G)$(ii)
 $(\sigma\otimes\text{id}_G)\circ \sigma = (\text{id}_X\otimes \delta_G)\circ \sigma$.
$(\sigma\otimes\text{id}_G)\circ \sigma = (\text{id}_X\otimes \delta_G)\circ \sigma$.
3. Skew product quivers
3.1. Definition of the skew product quiver
We wish to define a skew product quiver in analogy with the skew product graphs and skew product topological graphs studied to date [Reference Kaliszewski and Quigg10, Reference Kaliszewski, Quigg and Raeburn11]. So let ![]() $G$ be a locally compact group, and let
$G$ be a locally compact group, and let ![]() $\kappa:E^1\to G$ be a continuous map, called a of
$\kappa:E^1\to G$ be a continuous map, called a of ![]() $G$ on
$G$ on ![]() $\mathcal{Q}$. Then if
$\mathcal{Q}$. Then if ![]() $F^i=E^i\times G$ with continuous range map
$F^i=E^i\times G$ with continuous range map ![]() $r_\kappa(e,g)=(r(e),\kappa(e)g)$ and continuous, source map
$r_\kappa(e,g)=(r(e),\kappa(e)g)$ and continuous, source map ![]() $s_\kappa(e, g)=(s(e),g)$, we have most of the data required for a topological quiver. All that remains is to find a family of measures on
$s_\kappa(e, g)=(s(e),g)$, we have most of the data required for a topological quiver. All that remains is to find a family of measures on ![]() $F^1$ satisfying our conditions above. Since
$F^1$ satisfying our conditions above. Since ![]() $s^{-1}(v,g)= s^{-1}(v)\times \{g\}$, we define
$s^{-1}(v,g)= s^{-1}(v)\times \{g\}$, we define  $\lambda_\kappa=\{\lambda_{v,g}\}_{(v,g)\in F^0}$ by
$\lambda_\kappa=\{\lambda_{v,g}\}_{(v,g)\in F^0}$ by ![]() $\lambda_{v,g}(E)=\lambda_v(\{e\in E^1| (e,g)\in E\})$. First, we handle a technical lemma.
$\lambda_{v,g}(E)=\lambda_v(\{e\in E^1| (e,g)\in E\})$. First, we handle a technical lemma.
Lemma 3.1. Let ![]() $\xi\in C_c(E^1\times G)$ and
$\xi\in C_c(E^1\times G)$ and ![]() $(g_i)_{i\in I}$ a convergent net in
$(g_i)_{i\in I}$ a convergent net in ![]() $G$ with limit
$G$ with limit ![]() $g$. Then the net of functions
$g$. Then the net of functions ![]() $(\xi(\cdot, g_i))_{i\in I}$ converges uniformly to
$(\xi(\cdot, g_i))_{i\in I}$ converges uniformly to ![]() $\xi(\cdot, g)$.
$\xi(\cdot, g)$.
Proof. Certainly, ![]() $\xi(\cdot, g_i)$ converges pointwise to
$\xi(\cdot, g_i)$ converges pointwise to ![]() $\xi(\cdot, g)$ by the continuity of
$\xi(\cdot, g)$ by the continuity of ![]() $\xi$. The claim is that this convergence is uniform. Consider the space
$\xi$. The claim is that this convergence is uniform. Consider the space ![]() $K\times L\subset E^1\times G$ defined by
$K\times L\subset E^1\times G$ defined by ![]() $K=\text{proj}_{E^1}(\text{supp}(\xi))$ and
$K=\text{proj}_{E^1}(\text{supp}(\xi))$ and ![]() $L=\text{proj}_G(\text{supp}(\xi))$, which is a compact subset of the product. Choosing some precompact open set
$L=\text{proj}_G(\text{supp}(\xi))$, which is a compact subset of the product. Choosing some precompact open set ![]() $W$ in
$W$ in ![]() $E^1\times G$ containing the slice
$E^1\times G$ containing the slice ![]() $K\times \{g\}$, we apply the Tube Lemma [Reference Munkres17, Lemma 26.8] to
$K\times \{g\}$, we apply the Tube Lemma [Reference Munkres17, Lemma 26.8] to ![]() $W\cap K\times L$ find a product
$W\cap K\times L$ find a product ![]() $K\times V$ of open sets with
$K\times V$ of open sets with ![]() $K\times \{g\}\subset K\times V\subset W$. Writing
$K\times \{g\}\subset K\times V\subset W$. Writing ![]() $U=\text{proj}_{E^1}(W)$, the product
$U=\text{proj}_{E^1}(W)$, the product ![]() $U\times V$ is a precompact open set containing
$U\times V$ is a precompact open set containing ![]() $\text{supp}(\xi(\cdot, g))$.
$\text{supp}(\xi(\cdot, g))$.
We now claim that the family of functions  $\{\xi(\cdot, g)\}_{g\in \overline{V}}$ satisfies the hypotheses of Ascoli’s Theorem. That the family is pointwise bounded is clear, and equicontinuity follows from a standard
$\{\xi(\cdot, g)\}_{g\in \overline{V}}$ satisfies the hypotheses of Ascoli’s Theorem. That the family is pointwise bounded is clear, and equicontinuity follows from a standard ![]() $\epsilon/3$ argument. So the family of functions is precompact in
$\epsilon/3$ argument. So the family of functions is precompact in ![]() $C_0(E^1)$. Since the net
$C_0(E^1)$. Since the net ![]() $(\xi(\cdot, g_i))$ is eventually in the family, there is a convergent subnet for the uniform topology. Since the net converges pointwise to
$(\xi(\cdot, g_i))$ is eventually in the family, there is a convergent subnet for the uniform topology. Since the net converges pointwise to ![]() $\xi(\cdot, g)$, the net must converge uniformly to the same limit.
$\xi(\cdot, g)$, the net must converge uniformly to the same limit.
Proposition 3.2. The ensemble ![]() $\mathcal{Q}\times_\kappa G=\{F^0, F^1, r_\kappa, s_\kappa, \lambda_\kappa \}$ defines a topological quiver.
$\mathcal{Q}\times_\kappa G=\{F^0, F^1, r_\kappa, s_\kappa, \lambda_\kappa \}$ defines a topological quiver.
Proof. Clearly ![]() $r_\kappa$ and
$r_\kappa$ and ![]() $s_\kappa$ are continuous, with
$s_\kappa$ are continuous, with ![]() $s_\kappa$ an open map. Since
$s_\kappa$ an open map. Since
we have ![]() $\text{supp}(\lambda_{v, g}) = s^{-1}(v,g)$. So all that remains is to show that the family
$\text{supp}(\lambda_{v, g}) = s^{-1}(v,g)$. So all that remains is to show that the family ![]() $\lambda_\kappa$ is a continuous
$\lambda_\kappa$ is a continuous ![]() $s_\kappa$-system.
$s_\kappa$-system.
Let ![]() $\xi\in C_c(F^1)$ and take a net
$\xi\in C_c(F^1)$ and take a net ![]() $(v,g)_i=(v_i,g_i)$ converging to
$(v,g)_i=(v_i,g_i)$ converging to ![]() $(v, g)$ in
$(v, g)$ in ![]() $F^0$. Then compute
$F^0$. Then compute
 \begin{align*}
&\left|\int\xi\,\mathrm{d}\lambda_{v,g}-\int\xi\,\mathrm{d}\lambda_{v_i,g_i }\right|=\left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_{v}- \int \xi(\cdot, g_i)\,\mathrm{d}\lambda_{v_i}\right|\\
\leq& \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+\left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i} - \int \xi(\cdot, g_i)\,\mathrm{d}\lambda_{v_i}\right|\\
=& \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \left|\int \xi(\cdot, g)-\xi(\cdot, g_i)\,\mathrm{d}\lambda_{v_i}\right|\\
\leq& \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \int\left| \xi(\cdot, g)-\xi(\cdot, g_i)\right|\,\mathrm{d}\lambda_{v_i}.
\end{align*}
\begin{align*}
&\left|\int\xi\,\mathrm{d}\lambda_{v,g}-\int\xi\,\mathrm{d}\lambda_{v_i,g_i }\right|=\left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_{v}- \int \xi(\cdot, g_i)\,\mathrm{d}\lambda_{v_i}\right|\\
\leq& \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+\left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i} - \int \xi(\cdot, g_i)\,\mathrm{d}\lambda_{v_i}\right|\\
=& \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \left|\int \xi(\cdot, g)-\xi(\cdot, g_i)\,\mathrm{d}\lambda_{v_i}\right|\\
\leq& \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \int\left| \xi(\cdot, g)-\xi(\cdot, g_i)\right|\,\mathrm{d}\lambda_{v_i}.
\end{align*} We begin by analysing the second term above. Let ![]() $\epsilon \gt 0$. By Lemma 3.1, there is an index
$\epsilon \gt 0$. By Lemma 3.1, there is an index ![]() $i$ such that
$i$ such that ![]() $j\geq i$ implies
$j\geq i$ implies ![]() $\|\xi(\cdot, g)-\xi(\cdot, g_j)\|\leq \epsilon$. Meanwhile, by Urysohn’s Lemma, we may find a compactly supported function
$\|\xi(\cdot, g)-\xi(\cdot, g_j)\|\leq \epsilon$. Meanwhile, by Urysohn’s Lemma, we may find a compactly supported function ![]() $\eta$ with
$\eta$ with ![]() $\eta\equiv 1$ on
$\eta\equiv 1$ on ![]() $\text{proj}_{E^1}(\text{supp}(\xi))$. It now follows for the second term that sufficiently far along the sequence
$\text{proj}_{E^1}(\text{supp}(\xi))$. It now follows for the second term that sufficiently far along the sequence
 \begin{align*}
\int\left|\xi(\cdot, g)-\xi(\cdot, g_i)\right|\,\mathrm{d}\lambda_{v_i}
&\leq \int\epsilon \eta\,\mathrm{d}\lambda_{v_i} =\epsilon \int \eta\,\mathrm{d}\lambda_{v_i}
\end{align*}
\begin{align*}
\int\left|\xi(\cdot, g)-\xi(\cdot, g_i)\right|\,\mathrm{d}\lambda_{v_i}
&\leq \int\epsilon \eta\,\mathrm{d}\lambda_{v_i} =\epsilon \int \eta\,\mathrm{d}\lambda_{v_i}
\end{align*} which converges by continuity to ![]() $\epsilon \int\eta\,\mathrm{d}\lambda_v.$ Now,
$\epsilon \int\eta\,\mathrm{d}\lambda_v.$ Now,
 \begin{align*}&\left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \int\left| \xi(\cdot, g)-\xi(\cdot, g_i)\right|\,\mathrm{d}\lambda_{v_i}\\
\leq & \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \epsilon\int\eta\,\mathrm{d}\lambda_{v_i}\\
= & \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \epsilon\left( \int\eta\,\mathrm{d}\lambda_{v_i} - \int\eta\,\mathrm{d}\lambda_v\right) + \epsilon\left(\int\eta\,\mathrm{d}\lambda_v\right).
\end{align*}
\begin{align*}&\left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \int\left| \xi(\cdot, g)-\xi(\cdot, g_i)\right|\,\mathrm{d}\lambda_{v_i}\\
\leq & \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \epsilon\int\eta\,\mathrm{d}\lambda_{v_i}\\
= & \left|\int \xi(\cdot, g)\,\mathrm{d}\lambda_v - \int \xi(\cdot, g)\,\mathrm{d}\lambda_{v_i}\right|+ \epsilon\left( \int\eta\,\mathrm{d}\lambda_{v_i} - \int\eta\,\mathrm{d}\lambda_v\right) + \epsilon\left(\int\eta\,\mathrm{d}\lambda_v\right).
\end{align*} Now, each of the three terms vanish along the sequence by either continuity of the ![]() $s$-system or Lemma 3.1, establishing continuity for
$s$-system or Lemma 3.1, establishing continuity for ![]() $\lambda_\kappa$.
$\lambda_\kappa$.
Remark 3.3. Now that we have seen that ![]() $\mathcal{Q}\times_\kappa G$ is a topological quiver, observe how
$\mathcal{Q}\times_\kappa G$ is a topological quiver, observe how ![]() $G$ interacts with the skew product. The edge and vertex sets
$G$ interacts with the skew product. The edge and vertex sets ![]() $E^i\times G$ are trivial bundles over
$E^i\times G$ are trivial bundles over ![]() $G$, and we can associate with each individual space
$G$, and we can associate with each individual space ![]() $E^i\times G$ an action of
$E^i\times G$ an action of ![]() $G$ on the right by
$G$ on the right by ![]() $(e, h)\cdot g=(e, hg)$. Since
$(e, h)\cdot g=(e, hg)$. Since ![]() $G$ acts on itself and only on the second coordinate, this defines a principal
$G$ acts on itself and only on the second coordinate, this defines a principal ![]() $G$-bundle
$G$-bundle ![]() $q^i:F^i\to E^i$. In practice, we will freely write
$q^i:F^i\to E^i$. In practice, we will freely write ![]() $q$ to refer to either of these quotient maps. Moreover, the range and source maps each define
$q$ to refer to either of these quotient maps. Moreover, the range and source maps each define ![]() $G$-bundle morphisms from the edge spaces to the vertex spaces.
$G$-bundle morphisms from the edge spaces to the vertex spaces.
Since we have these quotient maps between topological spaces, we also have an induced non-degenerate ![]() $*$-homomorphism
$*$-homomorphism ![]() $C_0(E^0)\to M(C_0(F^0))$ by
$C_0(E^0)\to M(C_0(F^0))$ by ![]() $f\mapsto f\circ q$.
$f\mapsto f\circ q$.
3.2 A classification of skew products
In this section, we extend the notions of [Reference Deaconu, Kumjian and Quigg3, § 3] with the aim of showing that the only obstructions to a topological quiver being a skew product are the existence of a free and proper action by ![]() $G$ and a global section for the quotient. We remark that [Reference Deaconu, Kumjian and Quigg3] goes considerably further in their analysis of group actions on topological graphs, which we leave to pursue in future work.
$G$ and a global section for the quotient. We remark that [Reference Deaconu, Kumjian and Quigg3] goes considerably further in their analysis of group actions on topological graphs, which we leave to pursue in future work.
Given a topological quiver ![]() $\mathcal{Q}$, a locally compact group
$\mathcal{Q}$, a locally compact group ![]() $G$ and a cocycle
$G$ and a cocycle ![]() $\kappa:E^1\to G$, we have shown how to construct a skew product quiver. One lifts the associated structures (being the range map, source map and the
$\kappa:E^1\to G$, we have shown how to construct a skew product quiver. One lifts the associated structures (being the range map, source map and the ![]() $s$-system
$s$-system ![]() $\lambda$) to the appropriate trivial bundles
$\lambda$) to the appropriate trivial bundles ![]() $E^i\times G$, allowing some interference by the cocycle. Investigating this construction further, we have seen that each of the trivial bundles is equipped with a free and proper action of
$E^i\times G$, allowing some interference by the cocycle. Investigating this construction further, we have seen that each of the trivial bundles is equipped with a free and proper action of ![]() $G$ by right translation in the second variable, and that the quotient of each space by this action recovers the original edge and vertex spaces. Our first motions demonstrate the connection shared between these nominally distinct bundles.
$G$ by right translation in the second variable, and that the quotient of each space by this action recovers the original edge and vertex spaces. Our first motions demonstrate the connection shared between these nominally distinct bundles.
Definition 3.4. Given topological quivers ![]() $\mathcal{Q} = (E^0, E^1, r, s, \lambda), \mathcal{R} = (F^0, F^1, r, s, \mu)$, a quiver morphism
$\mathcal{Q} = (E^0, E^1, r, s, \lambda), \mathcal{R} = (F^0, F^1, r, s, \mu)$, a quiver morphism ![]() $\phi:\mathcal{Q}\to \mathcal{R}$ is a pair of continuous maps
$\phi:\mathcal{Q}\to \mathcal{R}$ is a pair of continuous maps ![]() $\phi = (\phi^0, \phi^1)$, where
$\phi = (\phi^0, \phi^1)$, where ![]() $\phi^0:E^0\to F^0$ and
$\phi^0:E^0\to F^0$ and ![]() $\phi^1:E^1\to F^1$ such that
$\phi^1:E^1\to F^1$ such that ![]() $r\circ\phi^1 = \phi^0\circ r$ and
$r\circ\phi^1 = \phi^0\circ r$ and ![]() $s\circ\phi^1 = \phi^1\circ s$.
$s\circ\phi^1 = \phi^1\circ s$.
An isomorphism of topological quivers is a quiver morphism with each map ![]() $(\phi^0, \phi^1)$ a homeomorphism and which preserves the measurements of the
$(\phi^0, \phi^1)$ a homeomorphism and which preserves the measurements of the ![]() $s$-system. By this, we mean that for every vertex
$s$-system. By this, we mean that for every vertex ![]() $v$ and every measurable set
$v$ and every measurable set ![]() $E\subseteq s^{-1}(v)$,
$E\subseteq s^{-1}(v)$,  $\lambda_v(E) = \mu_{\phi^0(v)}(\phi^1(E))$. It follows that the inverse pair
$\lambda_v(E) = \mu_{\phi^0(v)}(\phi^1(E))$. It follows that the inverse pair ![]() $\phi^{-1} = ((\phi^0)^{-1},(\phi^1)^{-1}) $ is also a quiver morphism. The group of all automorphisms of a topological quiver will be denoted by
$\phi^{-1} = ((\phi^0)^{-1},(\phi^1)^{-1}) $ is also a quiver morphism. The group of all automorphisms of a topological quiver will be denoted by ![]() $\text{Aut}(\mathcal{Q})$.
$\text{Aut}(\mathcal{Q})$.
A locally compact group acts on a topological quiver ![]() $\mathcal{Q}$ provided there is a continuous group homomorphism
$\mathcal{Q}$ provided there is a continuous group homomorphism ![]() $\alpha: G\to \text{Aut}\mathcal{Q}$, with
$\alpha: G\to \text{Aut}\mathcal{Q}$, with  $g\mapsto \alpha_g = (\alpha_g^0, \alpha_g^1)$. The vertex action
$g\mapsto \alpha_g = (\alpha_g^0, \alpha_g^1)$. The vertex action  $\alpha^0_g(v)$ will often be abbreviated by
$\alpha^0_g(v)$ will often be abbreviated by ![]() $g\cdot v$, and likewise for the edge action. The action is free provided it is free on the vertices; it follows that the action is free on the edges. The action is proper provided the translation map is proper on the vertex space. This is also enough to deduce properness of the action on the edge space by [Reference Anantharaman-Delaroche and Renault5, Proposition 2.1.14].
$g\cdot v$, and likewise for the edge action. The action is free provided it is free on the vertices; it follows that the action is free on the edges. The action is proper provided the translation map is proper on the vertex space. This is also enough to deduce properness of the action on the edge space by [Reference Anantharaman-Delaroche and Renault5, Proposition 2.1.14].
Example 3.5. Given a topological quiver ![]() $\mathcal{Q}$, group
$\mathcal{Q}$, group ![]() $G$ and a cocycle
$G$ and a cocycle ![]() $\kappa$, the skew product quiver
$\kappa$, the skew product quiver ![]() $\mathcal{Q}\times_\kappa G$ comes equipped with an action of
$\mathcal{Q}\times_\kappa G$ comes equipped with an action of ![]() $G$ by right translation on the second factor,
$G$ by right translation on the second factor, ![]() $(v, h)\cdot g = (v, hg)$. Indeed,
$(v, h)\cdot g = (v, hg)$. Indeed,
 \begin{align*}
s(e, h)\cdot g &= (s(e), h)\cdot g = (s(e), hg) = s(e, hg) = s((e,h)\cdot g),\\
r(e, h)\cdot g &= (r(e),\kappa(e)h)\cdot g = (r(e), \kappa(e)hg) = r(e, hg) = r((e, h)\cdot g),
\end{align*}
\begin{align*}
s(e, h)\cdot g &= (s(e), h)\cdot g = (s(e), hg) = s(e, hg) = s((e,h)\cdot g),\\
r(e, h)\cdot g &= (r(e),\kappa(e)h)\cdot g = (r(e), \kappa(e)hg) = r(e, hg) = r((e, h)\cdot g),
\end{align*} demonstrating covariance of the action with the range and source maps. Continuity is clear, and since right translation on a group is a free and proper action, it follows that the this action of ![]() $G$ on
$G$ on ![]() $\mathcal{Q}$ is both free and proper.
$\mathcal{Q}$ is both free and proper.
Given a free and proper action of a group on a topological quiver, it is easy to identify the quotient by this action.
Proposition 3.6. If a group ![]() $G$ acts freely and properly on a topological quiver
$G$ acts freely and properly on a topological quiver ![]() $\mathcal{Q}= (E^0, E^1, r, s, \lambda)$, then the ensemble
$\mathcal{Q}= (E^0, E^1, r, s, \lambda)$, then the ensemble ![]() $q(\mathcal{Q})= (q(E^0), q(E^1), \dot{r}, \dot{s}, \dot{\lambda})$ is a topological quiver.
$q(\mathcal{Q})= (q(E^0), q(E^1), \dot{r}, \dot{s}, \dot{\lambda})$ is a topological quiver.
Proof. Since ![]() $G$ acts freely and properly on the vertex and edge spaces the orbit spaces are locally compact Hausdorff, and the orbit maps
$G$ acts freely and properly on the vertex and edge spaces the orbit spaces are locally compact Hausdorff, and the orbit maps ![]() $q:E^i\to q(E^i)$, assigning the points to their orbits are quotient maps. The covariance of the range and source maps for the actions on the vertex and edge spaces guarantees unique continuous maps
$q:E^i\to q(E^i)$, assigning the points to their orbits are quotient maps. The covariance of the range and source maps for the actions on the vertex and edge spaces guarantees unique continuous maps ![]() $\dot{r}$ and
$\dot{r}$ and ![]() $\dot{s}$ given by composition with
$\dot{s}$ given by composition with ![]() $q$, and
$q$, and ![]() $\dot{s}$ remains open since compositions of open maps are open. Since the
$\dot{s}$ remains open since compositions of open maps are open. Since the ![]() $s$-system is equivariant by assumption, there is also an associated
$s$-system is equivariant by assumption, there is also an associated ![]() $\dot{s}$-system
$\dot{s}$-system ![]() $\dot{\lambda}$ by Theorem 2.8.
$\dot{\lambda}$ by Theorem 2.8.
Corollary 3.7. Given a skew product ![]() $\mathcal{Q}\times_\kappa G$, the quotient quiver
$\mathcal{Q}\times_\kappa G$, the quotient quiver ![]() $q(\mathcal{Q}\times_\kappa G)$ is isomorphic to
$q(\mathcal{Q}\times_\kappa G)$ is isomorphic to ![]() $\mathcal{Q}$.
$\mathcal{Q}$.
Proof. Since any skew product quiver ![]() $\mathcal{Q}\times_\kappa G$ is naturally equipped with a free and proper action, it follows from Proposition 3.6 that the quotient is another topological quiver. In this context, the orbit maps
$\mathcal{Q}\times_\kappa G$ is naturally equipped with a free and proper action, it follows from Proposition 3.6 that the quotient is another topological quiver. In this context, the orbit maps ![]() $q$ take the particularly simple form of projection onto the first factor of the products
$q$ take the particularly simple form of projection onto the first factor of the products ![]() $E^i\times G$, the quotient maps
$E^i\times G$, the quotient maps ![]() $\dot{r}, \dot{s}$ coincide with the range and source maps of the original quiver, and the equivariant system of measures agrees with the system from the original quiver, so that
$\dot{r}, \dot{s}$ coincide with the range and source maps of the original quiver, and the equivariant system of measures agrees with the system from the original quiver, so that ![]() $q(\mathcal{Q}\times_\kappa G)\cong \mathcal{Q}$.
$q(\mathcal{Q}\times_\kappa G)\cong \mathcal{Q}$.
So we see that given a quiver ![]() $\mathcal{Q}$, a group
$\mathcal{Q}$, a group ![]() $G$ and a cocycle
$G$ and a cocycle ![]() $\kappa:E^1\to G$, we can generate a new topological quiver
$\kappa:E^1\to G$, we can generate a new topological quiver ![]() $\mathcal{Q}\times_\kappa G$, and this quiver comes equipped with a free and proper action by
$\mathcal{Q}\times_\kappa G$, and this quiver comes equipped with a free and proper action by ![]() $G$. For the case of directed graphs and discrete groups, [Reference Gross and Tucker6, Theorem 2.2.2] shows that free actions by
$G$. For the case of directed graphs and discrete groups, [Reference Gross and Tucker6, Theorem 2.2.2] shows that free actions by ![]() $G$ are in one-to-one correspondence with the skew products by some cocycle (see also [Reference Deaconu, Kumjian and Quigg3, Corollary 3.7]). We have shown that for topological quivers, every skew product construction naturally associates a free and proper action by
$G$ are in one-to-one correspondence with the skew products by some cocycle (see also [Reference Deaconu, Kumjian and Quigg3, Corollary 3.7]). We have shown that for topological quivers, every skew product construction naturally associates a free and proper action by ![]() $G$, so we can ask under what criteria this free and proper action recovers the underlying quiver and cocycle. It turns out that there is only one.
$G$, so we can ask under what criteria this free and proper action recovers the underlying quiver and cocycle. It turns out that there is only one.
Theorem 3.8. Given a topological quiver ![]() $\mathcal{Q}$, a locally compact group
$\mathcal{Q}$, a locally compact group ![]() $G$ and a cocycle
$G$ and a cocycle ![]() $\kappa: E^1\to G$, the skew product quiver
$\kappa: E^1\to G$, the skew product quiver ![]() $\mathcal{Q}\times_\kappa G$ comes equipped with a free and proper action of
$\mathcal{Q}\times_\kappa G$ comes equipped with a free and proper action of ![]() $G$ by right translation in the second coordinate, and the quiver of orbits is isomorphic to the initial quiver
$G$ by right translation in the second coordinate, and the quiver of orbits is isomorphic to the initial quiver ![]() $\mathcal{Q}$.
$\mathcal{Q}$.
Conversely, suppose we are given a topological quiver ![]() $\mathcal{R}$ together with a free and proper action by a group
$\mathcal{R}$ together with a free and proper action by a group ![]() $G$. If the vertex orbit map
$G$. If the vertex orbit map ![]() $q:F^0\to q(F^0)$ is trivial as a
$q:F^0\to q(F^0)$ is trivial as a ![]() $G$-bundle (so that
$G$-bundle (so that ![]() $F^0\cong q(F^0) \times G$), then
$F^0\cong q(F^0) \times G$), then ![]() $\mathcal{R}$ is isomorphic to a skew product quiver.
$\mathcal{R}$ is isomorphic to a skew product quiver.
Proof. The first part is Corollary 3.7. We proceed with the other direction.
Denote the components of ![]() $\mathcal{R}$ by
$\mathcal{R}$ by ![]() $(F^0, F^1, r, s, \lambda)$, and the quiver of orbits by
$(F^0, F^1, r, s, \lambda)$, and the quiver of orbits by ![]() $q(\mathcal{R}) = (E^0, E^1, \dot{r},\dot{s},\dot{\lambda})$ which is guaranteed by Proposition 3.6. By hypothesis, we have an isomorphism
$q(\mathcal{R}) = (E^0, E^1, \dot{r},\dot{s},\dot{\lambda})$ which is guaranteed by Proposition 3.6. By hypothesis, we have an isomorphism
and we freely identify a vertex from ![]() $F^0$ with its image under
$F^0$ with its image under ![]() $\phi$. Since the source map
$\phi$. Since the source map ![]() $s$ is
$s$ is ![]() $G$-equivariant, Theorem 2.6 produces an isomorphism
$G$-equivariant, Theorem 2.6 produces an isomorphism ![]() $l$ from F 1 to the pullback
$l$ from F 1 to the pullback ![]() $E^1*_{\dot{s}} F^0$. Considering that the assignment
$E^1*_{\dot{s}} F^0$. Considering that the assignment ![]() $(e, (v,g) )\mapsto (e, g)$ with inverse
$(e, (v,g) )\mapsto (e, g)$ with inverse ![]() $(e, g)\mapsto (e, s(e), g)$ constructs a homeomorphism
$(e, g)\mapsto (e, s(e), g)$ constructs a homeomorphism ![]() $E^1*_{\dot{s}} G\to E^1\times G$, post-composition of
$E^1*_{\dot{s}} G\to E^1\times G$, post-composition of ![]() $l$ by this map constructs a homeomorphism
$l$ by this map constructs a homeomorphism
We claim that the following diagram commutes

It is clear that the bottom square commutes according to the definition of the central map ![]() $\dot{s}\times \text{id}$. Meanwhile, the right triangle commutes essentially by definition, and the left triangle commutes as a consequence of Theorem 2.6. For the top square, we compute that
$\dot{s}\times \text{id}$. Meanwhile, the right triangle commutes essentially by definition, and the left triangle commutes as a consequence of Theorem 2.6. For the top square, we compute that
where ![]() $f$ is the unique element of
$f$ is the unique element of ![]() $F^1$ associated to the data
$F^1$ associated to the data ![]() $(e, (s(e), g) )$ in
$(e, (s(e), g) )$ in ![]() $E^1*_s F^0$. Precomposition by
$E^1*_s F^0$. Precomposition by ![]() $\sigma$ in the expression above concludes the commutativity of the diagram.
$\sigma$ in the expression above concludes the commutativity of the diagram.
A similar argument shows that the analogous diagram for range maps also commutes, so that we have a commutative diagram

This diagram now suggests our candidate for a quiver isomorphism with a skew product. We define ![]() $\tilde{r} = (\dot{r}\times\text{id})\circ \rho\circ \sigma^{-1}$, define
$\tilde{r} = (\dot{r}\times\text{id})\circ \rho\circ \sigma^{-1}$, define  $\mathcal{Q}=(E^0\times G, E^1\times G, \tilde{r}, \dot{s}\times\text{id}, \{\lambda_{\phi(v)}\}_{v\in F^0})$, and then construct the quiver isomorphism
$\mathcal{Q}=(E^0\times G, E^1\times G, \tilde{r}, \dot{s}\times\text{id}, \{\lambda_{\phi(v)}\}_{v\in F^0})$, and then construct the quiver isomorphism
Indeed, the maps ![]() $\sigma$ and
$\sigma$ and ![]() $\phi$ are homeomorphisms by construction, and it is clear that at least the source maps factor through the isomorphism. As for the range map, we compute
$\phi$ are homeomorphisms by construction, and it is clear that at least the source maps factor through the isomorphism. As for the range map, we compute
verifying the range maps also factor through the isomorphism. The source map ![]() $\dot{s}\times \text{id} = \phi\circ s\circ \sigma^{-1}$ is open as a composition of open maps, and the
$\dot{s}\times \text{id} = \phi\circ s\circ \sigma^{-1}$ is open as a composition of open maps, and the ![]() $\dot{s}\times\text{id}$-system agrees with the original
$\dot{s}\times\text{id}$-system agrees with the original ![]() $s$-system up to identification of the vertices under
$s$-system up to identification of the vertices under ![]() $\phi$. Thus,
$\phi$. Thus, ![]() $(\sigma, \phi)$ is a quiver isomorphism.
$(\sigma, \phi)$ is a quiver isomorphism.
It remains to show that the image of this isomorphism is in fact a skew product. We claim that ![]() $\mathcal{Q}\cong q(\mathcal{R})\times_\kappa G$ for some cocycle
$\mathcal{Q}\cong q(\mathcal{R})\times_\kappa G$ for some cocycle ![]() $\kappa$. To find this cocycle, we investigate the edge space automorphism
$\kappa$. To find this cocycle, we investigate the edge space automorphism ![]() $\rho\circ \sigma^{-1}$.
$\rho\circ \sigma^{-1}$.
Since the inner diamond of the above diagram commutes, we know that ![]() $\text{pr}\circ\rho\circ\sigma^{-1} = \text{pr}$, so
$\text{pr}\circ\rho\circ\sigma^{-1} = \text{pr}$, so ![]() $\rho\circ\sigma^{-1}$ fixes the first factor. Since
$\rho\circ\sigma^{-1}$ fixes the first factor. Since ![]() $\rho$ and
$\rho$ and ![]() $\sigma$ are
$\sigma$ are ![]() $G$-equivariant, this map depends only on the choice of
$G$-equivariant, this map depends only on the choice of ![]() $e\in E^1$, and we define
$e\in E^1$, and we define ![]() $\kappa$ according to
$\kappa$ according to
where we treat 1 as the neutral element of the group. Now, let us identify ![]() $q(\mathcal{R})\times_\kappa G$. As spaces, the edge and vertex spaces are
$q(\mathcal{R})\times_\kappa G$. As spaces, the edge and vertex spaces are ![]() $E^1\times G$ and
$E^1\times G$ and ![]() $E^0\times G$, and the source map for the skew product is
$E^0\times G$, and the source map for the skew product is ![]() $(e, g)\mapsto (\dot{s}(e), g) = \dot{s}\times\text{id}(e, g)$. For the range map, we write
$(e, g)\mapsto (\dot{s}(e), g) = \dot{s}\times\text{id}(e, g)$. For the range map, we write
and compute
 \begin{align*}
(\dot{r}(e), \kappa(e)g) &=g(\dot{r}(e), \kappa(e))\\
&=g[\dot{r}\times\text{id}(e, \kappa(e))]\\
&=g[\dot{r}\times\text{id}(\rho\circ\sigma^{-1}(e, 1))]\\
&=g[\tilde{r}(e, 1)]\\
&=\tilde{r}(e, g)\\
\end{align*}
\begin{align*}
(\dot{r}(e), \kappa(e)g) &=g(\dot{r}(e), \kappa(e))\\
&=g[\dot{r}\times\text{id}(e, \kappa(e))]\\
&=g[\dot{r}\times\text{id}(\rho\circ\sigma^{-1}(e, 1))]\\
&=g[\tilde{r}(e, 1)]\\
&=\tilde{r}(e, g)\\
\end{align*} and verify that the range map for the skew product agrees with the range map defined for ![]() $\mathcal{Q}$. Finally, the equivariance of the
$\mathcal{Q}$. Finally, the equivariance of the ![]() $s$-system
$s$-system ![]() $\lambda$ under the group action guarantees that the orbit quiver has the
$\lambda$ under the group action guarantees that the orbit quiver has the ![]() $\dot{s}$-system
$\dot{s}$-system ![]() $\dot{\lambda}$, and the skew product quiver by construction reproduces an equivariant
$\dot{\lambda}$, and the skew product quiver by construction reproduces an equivariant ![]() $\dot{s}\times\text{id}$-system
$\dot{s}\times\text{id}$-system ![]() $\tilde{\lambda}$ which agrees with the original
$\tilde{\lambda}$ which agrees with the original ![]() $s$-system by the commutativity of the top-right square in the diagram. We thus conclude that
$s$-system by the commutativity of the top-right square in the diagram. We thus conclude that
 \begin{align*}
\mathcal{R} &= (F^0, F^1, s, r, \lambda)\\
&\cong (E^0\times G, E^1\times G, \dot{s}\times\text{id}, \tilde{r}, \tilde{\lambda})\\
&= \mathcal{Q}\\
&= q(\mathcal{R})\times_\kappa G,
\end{align*}
\begin{align*}
\mathcal{R} &= (F^0, F^1, s, r, \lambda)\\
&\cong (E^0\times G, E^1\times G, \dot{s}\times\text{id}, \tilde{r}, \tilde{\lambda})\\
&= \mathcal{Q}\\
&= q(\mathcal{R})\times_\kappa G,
\end{align*} and ![]() $\mathcal{R}$ is isomorphic to a skew-product quiver.
$\mathcal{R}$ is isomorphic to a skew-product quiver.
4. Coactions and skew products
Throughout this section, we fix a topological quiver ![]() $\mathcal{Q}$ together with a cocycle
$\mathcal{Q}$ together with a cocycle ![]() $\kappa:E^1\to G$ and write
$\kappa:E^1\to G$ and write ![]() $(X,A)$ for the correspondence associated with
$(X,A)$ for the correspondence associated with ![]() $\mathcal{Q}$. Furthermore, we write
$\mathcal{Q}$. Furthermore, we write ![]() $(Y, B)$ for the correspondence associated with
$(Y, B)$ for the correspondence associated with ![]() $\mathcal{Q}\times_\kappa G$.
$\mathcal{Q}\times_\kappa G$.
Dual to the skew product construction for topological quivers, a cocycle also determines an action by pointwise multiplication of ![]() $C_0(G)$ on
$C_0(G)$ on ![]() $(X,\,\, A)$ according to the induced homomorphism
$(X,\,\, A)$ according to the induced homomorphism ![]() $\kappa^*:C_0(G)\to M(C_0(E^1) )$. It is clear that this action commutes with the action coming from the range map, since their image is in the representation of
$\kappa^*:C_0(G)\to M(C_0(E^1) )$. It is clear that this action commutes with the action coming from the range map, since their image is in the representation of ![]() $C_0(E^1)$ in
$C_0(E^1)$ in ![]() $\mathcal{L}(X)$.
$\mathcal{L}(X)$.
Since ![]() $\kappa^*$ is a homomorphism of
$\kappa^*$ is a homomorphism of ![]() $C_0(G)$, we also have a homomorphism
$C_0(G)$, we also have a homomorphism
since ![]() $\kappa^*$ is non-degenerate (that is,
$\kappa^*$ is non-degenerate (that is, ![]() $\overline{\text{span}}(\kappa^*(C_0(G))\cdot A') = A'$). Define
$\overline{\text{span}}(\kappa^*(C_0(G))\cdot A') = A'$). Define ![]() $v\in M(A'\otimes C^* (G) )$ a unitary by
$v\in M(A'\otimes C^* (G) )$ a unitary by ![]() $v=\overline{\kappa^*\otimes\text{id}}(w_G)$.
$v=\overline{\kappa^*\otimes\text{id}}(w_G)$.
Remark 4.1. Because of the identification ![]() $M(C_0(X)\otimes C^* (G) )\cong C_b(X,M^\beta (C^* (G)) )$, we recognize
$M(C_0(X)\otimes C^* (G) )\cong C_b(X,M^\beta (C^* (G)) )$, we recognize ![]() $v$ as the function
$v$ as the function ![]() $v:E^1\to M^\beta(C^* (G) )$ with
$v:E^1\to M^\beta(C^* (G) )$ with ![]() $v(e)= \iota(\kappa(e)) $. So
$v(e)= \iota(\kappa(e)) $. So ![]() $v$ provides a
$v$ provides a ![]() ${C^*}$-algebraic expression of the cocycle on the associated correspondence.
${C^*}$-algebraic expression of the cocycle on the associated correspondence.
Proposition 4.2. Given a cocycle ![]() $\kappa$ of
$\kappa$ of ![]() $G$ on
$G$ on ![]() $\mathcal{Q}$, there is an (X, A) correspondence coaction
$\mathcal{Q}$, there is an (X, A) correspondence coaction ![]() $\sigma$ by
$\sigma$ by ![]() $G$ on
$G$ on ![]() $X$ defined by
$X$ defined by ![]() $\sigma(\xi) =v\cdot(\xi\otimes 1)$.
$\sigma(\xi) =v\cdot(\xi\otimes 1)$.
Moreover, ![]() $\sigma$ induces a coaction
$\sigma$ induces a coaction ![]() $\zeta$ by
$\zeta$ by ![]() $G$ on
$G$ on ![]() $C^*(\mathcal{Q})$ which is determined on generators by
$C^*(\mathcal{Q})$ which is determined on generators by
 \begin{align*}
\zeta\circ k_X (\xi)&= \overline{k_X\otimes\text{id}}\circ\sigma (\xi)\\
\zeta\circ k_A (\xi)&= k_A\otimes\text{id}\\
\end{align*}
\begin{align*}
\zeta\circ k_X (\xi)&= \overline{k_X\otimes\text{id}}\circ\sigma (\xi)\\
\zeta\circ k_A (\xi)&= k_A\otimes\text{id}\\
\end{align*} where ![]() $(k_X, k_A)$ is the universal representation of
$(k_X, k_A)$ is the universal representation of ![]() $(X, A)$ in
$(X, A)$ in ![]() $C^*(\mathcal{Q})$.
$C^*(\mathcal{Q})$.
Proof. Put ![]() $M:A'\to \mathcal{L}(X)$ the multiplication representation defined by
$M:A'\to \mathcal{L}(X)$ the multiplication representation defined by ![]() $[M(f)\xi](e) = f(e)\xi(e)$. Because
$[M(f)\xi](e) = f(e)\xi(e)$. Because ![]() $X$ is non-degenerate as an
$X$ is non-degenerate as an ![]() $A-A$ correspondence, the results of [Reference Kaliszewski, Quigg and Robertson13] apply. In particular, since
$A-A$ correspondence, the results of [Reference Kaliszewski, Quigg and Robertson13] apply. In particular, since ![]() $\mu=M\circ\kappa^*$ commutes with
$\mu=M\circ\kappa^*$ commutes with ![]() $\phi_A$, we apply [Reference Kaliszewski, Quigg and Robertson13, Corollary 3.5] to generate
$\phi_A$, we apply [Reference Kaliszewski, Quigg and Robertson13, Corollary 3.5] to generate ![]() $\zeta$.
$\zeta$.
With this coaction in hand, we may generate the coaction crossed product ![]() $C^*(\mathcal{Q})\times_\zeta G$ following the theory introduced in the preliminaries. Our main purpose is to show that this crossed product agrees with the
$C^*(\mathcal{Q})\times_\zeta G$ following the theory introduced in the preliminaries. Our main purpose is to show that this crossed product agrees with the ![]() ${C^*}$-algebra associated with the skew product quiver.
${C^*}$-algebra associated with the skew product quiver.
Theorem 4.3. ![]() $C^*(\mathcal{Q})\times_\zeta G \cong C^*(\mathcal{Q}\times_\kappa G)$.
$C^*(\mathcal{Q})\times_\zeta G \cong C^*(\mathcal{Q}\times_\kappa G)$.
Remark 4.4. Here is our strategy to prove this theorem. We will first produce a covariant representation ![]() $(\Pi,\psi): (C^*(\mathcal{Q}),\zeta)\to M(C^*(\mathcal{Q}\times_\kappa G)$, thereby generating a unique homomorphism
$(\Pi,\psi): (C^*(\mathcal{Q}),\zeta)\to M(C^*(\mathcal{Q}\times_\kappa G)$, thereby generating a unique homomorphism
Then, we will invoke the Dual Invariant Uniqueness Theorem [Reference Huef, Quigg, Raeburn and Williams8, Theorem 5.4] to show that the integrated form is injective. To achieve this end, our approach will be through a series of lemmas and propositions. As a guide, it may be constructive to consult the following diagram:

We begin with the construction of the homomorphism ![]() $\Pi$, which will require the most significant resources.
$\Pi$, which will require the most significant resources.
Proposition 4.5. There is a Cuntz–Pimsner covariant homomorphism ![]() $(\mu, \nu): (X,A)\to (M(Y), M(B))$. By the functoriality of Cuntz–Pimsner covariance [Reference Kaliszewski, Quigg and Robertson12], there is a unique associated homomorphism
$(\mu, \nu): (X,A)\to (M(Y), M(B))$. By the functoriality of Cuntz–Pimsner covariance [Reference Kaliszewski, Quigg and Robertson12], there is a unique associated homomorphism ![]() $\Pi:C^*(\mathcal{Q})\to M(C^*(\mathcal{Q}\times_\kappa G))$.
$\Pi:C^*(\mathcal{Q})\to M(C^*(\mathcal{Q}\times_\kappa G))$.
We define ![]() $\nu:A\to M(B)$ according to
$\nu:A\to M(B)$ according to ![]() $\nu:f\mapsto f\circ q$ and turn our attention to the map
$\nu:f\mapsto f\circ q$ and turn our attention to the map ![]() $\mu$. Throughout this discussion, fix
$\mu$. Throughout this discussion, fix ![]() $\xi\in C_c(E^1)$ and
$\xi\in C_c(E^1)$ and ![]() $f\in C_c(F^0)$.
$f\in C_c(F^0)$.
Lemma 4.6. The function ![]() $(\xi\circ q) \cdot (f\circ s): F^1\to \mathbb{C}$ has compact support.
$(\xi\circ q) \cdot (f\circ s): F^1\to \mathbb{C}$ has compact support.
Proof. Let ![]() $K=\text{supp}(\xi)\subseteq E^1$ and
$K=\text{supp}(\xi)\subseteq E^1$ and ![]() $L=\text{supp}(f)\subseteq F^0$. We may identify
$L=\text{supp}(f)\subseteq F^0$. We may identify ![]() $F^1$ with
$F^1$ with ![]() $E^1*_s F^0$ by the map
$E^1*_s F^0$ by the map ![]() $(e,g)\mapsto (e, s(e), g)$ by Theorem 2.6. Then
$(e,g)\mapsto (e, s(e), g)$ by Theorem 2.6. Then
is compact in ![]() $E^1*_sF^0\cong F^1$. This is exactly the support of
$E^1*_sF^0\cong F^1$. This is exactly the support of ![]() $\xi\circ q \cdot f\circ s$.
$\xi\circ q \cdot f\circ s$.
Lemma 4.7. The map ![]() $\mu(\xi): C_c(F^0)\to C_c(F^1)$ defined by
$\mu(\xi): C_c(F^0)\to C_c(F^1)$ defined by ![]() $\mu(\xi)\cdot f = \xi\circ q\cdot f\circ s$ is uniform to Hilbert-norm bounded and hence extends to a bimodule map
$\mu(\xi)\cdot f = \xi\circ q\cdot f\circ s$ is uniform to Hilbert-norm bounded and hence extends to a bimodule map ![]() $\mu(\xi): B\to Y$.
$\mu(\xi): B\to Y$.
Proof. Lemma 4.6 shows that ![]() $\mu(\xi)$ is well defined, and linearity is clear. So see that
$\mu(\xi)$ is well defined, and linearity is clear. So see that
 \begin{align*}
\langle\mu(\xi)\cdot f, \mu(\xi)\cdot f\rangle(v,g) &= \int \overline{(\xi\circ q)\cdot (f\circ s)}\cdot(\xi\circ q)\cdot (f\circ s)\,\mathrm{d}\lambda_{v,g}\\
&= \int |\xi\circ q|^2|f\circ s|^2\,\mathrm{d}\lambda_{v,g}\\
&= \langle\xi, \xi \rangle (q(v,g))|f(v,g)|^2\leq \|\xi\|^2\|f\|_u^2.\\
\end{align*}
\begin{align*}
\langle\mu(\xi)\cdot f, \mu(\xi)\cdot f\rangle(v,g) &= \int \overline{(\xi\circ q)\cdot (f\circ s)}\cdot(\xi\circ q)\cdot (f\circ s)\,\mathrm{d}\lambda_{v,g}\\
&= \int |\xi\circ q|^2|f\circ s|^2\,\mathrm{d}\lambda_{v,g}\\
&= \langle\xi, \xi \rangle (q(v,g))|f(v,g)|^2\leq \|\xi\|^2\|f\|_u^2.\\
\end{align*} Since this holds for all vertices ![]() $(v, g)$, we see that
$(v, g)$, we see that
So ![]() $\mu(\xi)$ is bounded and thus extends uniquely to a bounded linear map
$\mu(\xi)$ is bounded and thus extends uniquely to a bounded linear map ![]() $B\to Y$.
$B\to Y$.
Proposition 4.8. There is a Hilbert to uniform-norm bounded map ![]() $\mu(\xi)^*: C_c(F^1)\to C_c(F^0)$. Moreover, the unique continuous linear extension is an adjoint for
$\mu(\xi)^*: C_c(F^1)\to C_c(F^0)$. Moreover, the unique continuous linear extension is an adjoint for ![]() $\mu(\xi)$.
$\mu(\xi)$.
Proof. Fix ![]() $\eta\in C_c(F^1)$ and define
$\eta\in C_c(F^1)$ and define ![]() $\mu(\xi)^*$ by
$\mu(\xi)^*$ by
 \begin{equation*}\mu(\xi)^*\cdot \eta (v,g) = \int \overline{\xi\circ q (\alpha, g)}\eta(\alpha, g)\,\mathrm{d}\lambda_{v,g}(\alpha, g).\end{equation*}
\begin{equation*}\mu(\xi)^*\cdot \eta (v,g) = \int \overline{\xi\circ q (\alpha, g)}\eta(\alpha, g)\,\mathrm{d}\lambda_{v,g}(\alpha, g).\end{equation*} Notice that the restriction of ![]() $\xi\circ q$ to
$\xi\circ q$ to ![]() $s^{-1}(v,g)$ (and we will denote all such restrictions by, e.g.
$s^{-1}(v,g)$ (and we will denote all such restrictions by, e.g. ![]() $\xi\circ q |$) agrees with the restriction of ξ to
$\xi\circ q |$) agrees with the restriction of ξ to ![]() $s^{-1}(v)$ so that
$s^{-1}(v)$ so that ![]() $\xi\circ q|\in C_c(s^{-1}(v,g))$, and
$\xi\circ q|\in C_c(s^{-1}(v,g))$, and ![]() $\mu(\xi)^*\cdot \eta (v,g) = \langle \xi\circ q|, \eta|\rangle$, the inner product for
$\mu(\xi)^*\cdot \eta (v,g) = \langle \xi\circ q|, \eta|\rangle$, the inner product for ![]() $(L^2(F^1), \lambda_{v,g})$. Then
$(L^2(F^1), \lambda_{v,g})$. Then
 \begin{align*}
|\mu(\xi)^*\cdot \eta(v,g)|^2 &= |\langle \xi\circ q|, \eta|\rangle|^2\leq \left[\int|\xi\circ q|^2\,\mathrm{d}\lambda_{v,g}\right]\cdot \left[\int |\eta|^2 \,\mathrm{d}\lambda_{v,g}\right]\\
&=\langle\xi\circ q, \xi\circ q\rangle(v,g)\cdot \langle\eta,\eta\rangle(v,g)\leq \|\xi\|^2\cdot\|\eta\|^2,
\end{align*}
\begin{align*}
|\mu(\xi)^*\cdot \eta(v,g)|^2 &= |\langle \xi\circ q|, \eta|\rangle|^2\leq \left[\int|\xi\circ q|^2\,\mathrm{d}\lambda_{v,g}\right]\cdot \left[\int |\eta|^2 \,\mathrm{d}\lambda_{v,g}\right]\\
&=\langle\xi\circ q, \xi\circ q\rangle(v,g)\cdot \langle\eta,\eta\rangle(v,g)\leq \|\xi\|^2\cdot\|\eta\|^2,
\end{align*} so ![]() $\mu(\xi)^*\eta$ is bounded from
$\mu(\xi)^*\eta$ is bounded from ![]() $C_c(F^1)$ with the Hilbert norm to
$C_c(F^1)$ with the Hilbert norm to ![]() $C_c(F^0)$ with the uniform norm. So
$C_c(F^0)$ with the uniform norm. So ![]() $\mu(\xi)^*$ extends uniquely to
$\mu(\xi)^*$ extends uniquely to ![]() $\mu(\xi)^*: Y\to B$.
$\mu(\xi)^*: Y\to B$.
Lastly, to check adjoints, for ![]() $f\in C_0(F^0)$,
$f\in C_0(F^0)$,
 \begin{align*}
&\langle\mu(\xi)^*\cdot\eta, f\rangle(v,g) =\overline{\int \overline{\xi\circ q}\cdot \eta \,\mathrm{d}\lambda_{v,g}}\cdot f(v,g) = \int (\xi\circ q)\cdot \overline{\eta}\,\mathrm{d}\lambda_{v,g}\cdot f(v,g)\\
&=\int (\xi\circ q) \cdot \overline{\eta} \cdot f\circ s\,\mathrm{d}\lambda_{v,g} = \langle\eta, (\xi\circ q)\cdot (f\circ s)\rangle(v,g) = \langle\eta, \mu(\xi)\cdot f\rangle(v,g).
\end{align*}
\begin{align*}
&\langle\mu(\xi)^*\cdot\eta, f\rangle(v,g) =\overline{\int \overline{\xi\circ q}\cdot \eta \,\mathrm{d}\lambda_{v,g}}\cdot f(v,g) = \int (\xi\circ q)\cdot \overline{\eta}\,\mathrm{d}\lambda_{v,g}\cdot f(v,g)\\
&=\int (\xi\circ q) \cdot \overline{\eta} \cdot f\circ s\,\mathrm{d}\lambda_{v,g} = \langle\eta, (\xi\circ q)\cdot (f\circ s)\rangle(v,g) = \langle\eta, \mu(\xi)\cdot f\rangle(v,g).
\end{align*} It follows that ![]() $\mu(\xi)^*$ is an adjoint for
$\mu(\xi)^*$ is an adjoint for ![]() $\mu(\xi)$.
$\mu(\xi)$.
Remark 4.9. It now follows that ![]() $\mu(\xi)\in \mathcal{L}(B, Y) = M(Y)$ for any
$\mu(\xi)\in \mathcal{L}(B, Y) = M(Y)$ for any ![]() $\xi\in C_c(E^1)$. Since the map
$\xi\in C_c(E^1)$. Since the map ![]() $\mu:C_c(E^1)\to M(Y)$ is bounded by (4.2),
$\mu:C_c(E^1)\to M(Y)$ is bounded by (4.2), ![]() $\mu$ extends to a linear map
$\mu$ extends to a linear map ![]() $\mu:X\to M(Y)$. Now, for any
$\mu:X\to M(Y)$. Now, for any ![]() $\xi\in X$, we already have a natural right action of B on
$\xi\in X$, we already have a natural right action of B on ![]() $\mu(\xi)$ given by evaluation, but we also have a left action of
$\mu(\xi)$ given by evaluation, but we also have a left action of ![]() $B$ on
$B$ on ![]() $\mu(\xi)$, defined by
$\mu(\xi)$, defined by ![]() $f\cdot \mu(\xi) = (f\circ r)\cdot (\xi\circ q)$. Arguments analogous to the proofs of Lemmas 4.6 and 4.7 show that
$f\cdot \mu(\xi) = (f\circ r)\cdot (\xi\circ q)$. Arguments analogous to the proofs of Lemmas 4.6 and 4.7 show that ![]() $f\cdot \mu(\xi)\in Y$, and thus
$f\cdot \mu(\xi)\in Y$, and thus ![]() $\mu$ maps
$\mu$ maps ![]() $X$ to the relative multiplier algebra
$X$ to the relative multiplier algebra ![]() $M_B(Y)$.
$M_B(Y)$.
Proposition 4.10. The pair ![]() $(\mu,\nu):(X,A)\to (M(Y), M(B))$ is a correspondence homomorphism.
$(\mu,\nu):(X,A)\to (M(Y), M(B))$ is a correspondence homomorphism.
Proof. It suffices to confirm that ![]() $\langle \mu(\upsilon), \mu(\xi)\rangle = \nu(\langle\upsilon, \xi\rangle)$, and that
$\langle \mu(\upsilon), \mu(\xi)\rangle = \nu(\langle\upsilon, \xi\rangle)$, and that ![]() $\mu(f\cdot \xi) = \nu(f)\cdot\mu(\xi)$. We first check covariance of the left action, by computing
$\mu(f\cdot \xi) = \nu(f)\cdot\mu(\xi)$. We first check covariance of the left action, by computing
 \begin{align*}
\mu(f\cdot \xi) &= (f\circ r\cdot \xi)\circ q = (f\circ r)\circ q )\cdot (\xi\circ q)\\
&= (f\circ q)\circ r\cdot (\xi\circ q) = \nu(f)\cdot \mu(\xi).
\end{align*}
\begin{align*}
\mu(f\cdot \xi) &= (f\circ r\cdot \xi)\circ q = (f\circ r)\circ q )\cdot (\xi\circ q)\\
&= (f\circ q)\circ r\cdot (\xi\circ q) = \nu(f)\cdot \mu(\xi).
\end{align*} To confirm the relationships between the inner products, we first choose ![]() $f\in B$ and compute that for any vertex
$f\in B$ and compute that for any vertex ![]() $(v, g)$,
$(v, g)$,
 \begin{align*}
\langle \mu(\eta), \mu(\xi)\rangle\cdot f(v,g) &=\mu(\eta)^*\mu(\xi)\cdot f (v,g) = \mu(\eta)^*[\xi\circ q\cdot f\circ s](v,g)\\
&= \int \overline{\eta\circ q}\cdot (\xi\circ q)\cdot(f\circ s) \,\mathrm{d}\lambda_{v,g} = \int\overline{\eta\circ q}\cdot (\xi\circ q)\,\mathrm{d}\lambda_{v,g} f(v,g)\\
&=\int (\overline{\eta}\cdot\xi)\circ q\,\mathrm{d}\lambda_{v,g} f(v,g) = \left[\int \overline{\eta}\cdot \xi\, d\lambda_v\right]\circ q \cdot f(v,g)\\
&= \langle\eta, \xi\rangle \circ q \cdot f(v,g) = \nu(\langle\eta, \xi\rangle)\cdot f(v,g).
\end{align*}
\begin{align*}
\langle \mu(\eta), \mu(\xi)\rangle\cdot f(v,g) &=\mu(\eta)^*\mu(\xi)\cdot f (v,g) = \mu(\eta)^*[\xi\circ q\cdot f\circ s](v,g)\\
&= \int \overline{\eta\circ q}\cdot (\xi\circ q)\cdot(f\circ s) \,\mathrm{d}\lambda_{v,g} = \int\overline{\eta\circ q}\cdot (\xi\circ q)\,\mathrm{d}\lambda_{v,g} f(v,g)\\
&=\int (\overline{\eta}\cdot\xi)\circ q\,\mathrm{d}\lambda_{v,g} f(v,g) = \left[\int \overline{\eta}\cdot \xi\, d\lambda_v\right]\circ q \cdot f(v,g)\\
&= \langle\eta, \xi\rangle \circ q \cdot f(v,g) = \nu(\langle\eta, \xi\rangle)\cdot f(v,g).
\end{align*} Since ![]() $f$ and
$f$ and ![]() $(v, g)$ were arbitrary, the result follows.
$(v, g)$ were arbitrary, the result follows.
With this correspondence homomorphism now in hand, we now turn our attention to Cuntz–Pimsner covariance for this homomorphism.
Lemma 4.11. We have ![]() $\nu(J_X)\subseteq M(B; J_Y)$.
$\nu(J_X)\subseteq M(B; J_Y)$.
Proof. For topological quivers, the ideal ![]() $J_X$ is characterized in the preliminaries as
$J_X$ is characterized in the preliminaries as  $J_X=C_0(E^0_{\text{rg}})$, the set of regular vertices of the topological quiver. It suffices to show that for any
$J_X=C_0(E^0_{\text{rg}})$, the set of regular vertices of the topological quiver. It suffices to show that for any  $f\in J_X = C_0(E^0_\text{rg})$ and
$f\in J_X = C_0(E^0_\text{rg})$ and ![]() $b\in B$, we have
$b\in B$, we have ![]() $\nu(f)\cdot b \in J_Y$. So suppose
$\nu(f)\cdot b \in J_Y$. So suppose ![]() $\nu(f)\cdot b(v,g)\neq 0$, and we will show that
$\nu(f)\cdot b(v,g)\neq 0$, and we will show that ![]() $(v, g)$ is a regular vertex of
$(v, g)$ is a regular vertex of ![]() $\mathcal{Q}\times_\kappa G$. It follows that
$\mathcal{Q}\times_\kappa G$. It follows that ![]() $f\circ q (v,g) = f(v)\neq 0$, so
$f\circ q (v,g) = f(v)\neq 0$, so  $v\in E^0_\text{rg}$. Since
$v\in E^0_\text{rg}$. Since ![]() $v$ is not a sink, we can easily find an edge emitted by
$v$ is not a sink, we can easily find an edge emitted by ![]() $(v, g)$. Meanwhile, we may choose a suitable compact neighbourhood
$(v, g)$. Meanwhile, we may choose a suitable compact neighbourhood ![]() $W\subseteq E^0$ of
$W\subseteq E^0$ of ![]() $v$ with
$v$ with ![]() $r^{-1}(W)\subseteq E^1$ compact and
$r^{-1}(W)\subseteq E^1$ compact and ![]() $s$ restricted to this subset a local homeomorphism.
$s$ restricted to this subset a local homeomorphism.
Define a compact subset ![]() $U=W\times V$ of
$U=W\times V$ of ![]() $E^0\times G$. We claim that
$E^0\times G$. We claim that ![]() $U$ is a precompact neighbourhood of
$U$ is a precompact neighbourhood of ![]() $(v, g)$ which has
$(v, g)$ which has ![]() $r^{-1}(\overline{U})$ compact and
$r^{-1}(\overline{U})$ compact and  $s|_{r^{-1}(U)}$ a local homeomorphism.
$s|_{r^{-1}(U)}$ a local homeomorphism. ![]() $U$ is closed, so
$U$ is closed, so ![]() $r^{-1}(\overline{U})=r^{-1}(U)$ is closed in
$r^{-1}(\overline{U})=r^{-1}(U)$ is closed in ![]() $E^1\times G$. Moreover, if
$E^1\times G$. Moreover, if ![]() $(e, g)\in r^{-1}(U)$, then
$(e, g)\in r^{-1}(U)$, then ![]() $r(e, g) = (r(e), k(e)g)$, and it follows that
$r(e, g) = (r(e), k(e)g)$, and it follows that
Note that since the second factor in the above product is compact, and thus ![]() $r^{-1}(U)$ is compact. So it remains to show that the restriction of the source map to
$r^{-1}(U)$ is compact. So it remains to show that the restriction of the source map to ![]() $r^{-1}(U)$ is a local homeomorphism. This is easy, since the source map acts like the source map for
$r^{-1}(U)$ is a local homeomorphism. This is easy, since the source map acts like the source map for ![]() $\mathcal{Q}$ on the first factor and the identity on the second factor, so the restriction is the coordinatewise product of a local homeomorphism and a global homeomorphism.
$\mathcal{Q}$ on the first factor and the identity on the second factor, so the restriction is the coordinatewise product of a local homeomorphism and a global homeomorphism.
Lemma 4.12. The diagram commutes.

Proof. Choose ![]() $f\in J_X$ and fix
$f\in J_X$ and fix ![]() $\epsilon \gt 0$. Then there is a finite-rank operator
$\epsilon \gt 0$. Then there is a finite-rank operator ![]() $\Theta=\sum \theta_{\eta_k, \xi_k}\in \mathbb{K}(X)$ with
$\Theta=\sum \theta_{\eta_k, \xi_k}\in \mathbb{K}(X)$ with ![]() $\|\phi_A(f)-\Theta\| \lt \epsilon$. Now, for any
$\|\phi_A(f)-\Theta\| \lt \epsilon$. Now, for any ![]() $y\in C_c(F^1)$, we compute that
$y\in C_c(F^1)$, we compute that
 \begin{align*}
&\left\|[\mu^{(1)}\circ \phi_A(f)]y-[\bar{\phi}_B|\circ\nu]y\right\|\\
&\leq\left\|[\mu^{(1)}\circ\phi_A(f)]y-[\mu^{(1)}(\Theta)]y\right\|+\left\|\mu^{(1)}(\Theta)y-[\bar{\phi}_B|\circ \nu]y\right\|\\
&\leq \epsilon\|y\| + \left\|\mu^{(1)}(\Theta)y-[\bar{\phi}_B|\circ \nu]y\right\|,
\end{align*}
\begin{align*}
&\left\|[\mu^{(1)}\circ \phi_A(f)]y-[\bar{\phi}_B|\circ\nu]y\right\|\\
&\leq\left\|[\mu^{(1)}\circ\phi_A(f)]y-[\mu^{(1)}(\Theta)]y\right\|+\left\|\mu^{(1)}(\Theta)y-[\bar{\phi}_B|\circ \nu]y\right\|\\
&\leq \epsilon\|y\| + \left\|\mu^{(1)}(\Theta)y-[\bar{\phi}_B|\circ \nu]y\right\|,
\end{align*}so that what remains is to bound the second addend. To this end, we see
 \begin{equation*}\mu^{(1)}(\Theta)y = \mu^{(1)}(\sum\theta_{\eta_k, \xi_k})y = \left[\sum\mu(\eta_k)\mu(\xi_k)^*\right]y,\end{equation*}
\begin{equation*}\mu^{(1)}(\Theta)y = \mu^{(1)}(\sum\theta_{\eta_k, \xi_k})y = \left[\sum\mu(\eta_k)\mu(\xi_k)^*\right]y,\end{equation*}and by evaluating pointwise, that
 \begin{align*}
\mu^{(1)}(\Theta)y(e,g) &= \sum \eta_k\circ q(e, g)\cdot \int \overline{\xi_k\circ q}(\alpha,g)y(\alpha, g)\,\mathrm{d}\lambda_{s(e), g}\\
&=\sum \eta_k(e)\cdot \int \overline{\xi_k}(\alpha) y(\alpha, g)\,\mathrm{d}\lambda_{s(e)} = \left[\sum \eta_k\langle\xi_k, y(\cdot, g)\rangle\right](e)\\
&=\Theta(y(\cdot, g))(e).
\end{align*}
\begin{align*}
\mu^{(1)}(\Theta)y(e,g) &= \sum \eta_k\circ q(e, g)\cdot \int \overline{\xi_k\circ q}(\alpha,g)y(\alpha, g)\,\mathrm{d}\lambda_{s(e), g}\\
&=\sum \eta_k(e)\cdot \int \overline{\xi_k}(\alpha) y(\alpha, g)\,\mathrm{d}\lambda_{s(e)} = \left[\sum \eta_k\langle\xi_k, y(\cdot, g)\rangle\right](e)\\
&=\Theta(y(\cdot, g))(e).
\end{align*}On the other hand,
 \begin{align*}
[\bar{\phi}_B|\circ\nu](f)y(e,g) &= [\bar{\phi}_B| (f\circ q) y](e,g) = (f\circ q \circ r)(e,g)\cdot y(e,g) \\
&= (f\circ r\circ q)(e, g)\cdot y(e,g) = [\phi_A(f) y(\cdot, g)] (e), \\
\end{align*}
\begin{align*}
[\bar{\phi}_B|\circ\nu](f)y(e,g) &= [\bar{\phi}_B| (f\circ q) y](e,g) = (f\circ q \circ r)(e,g)\cdot y(e,g) \\
&= (f\circ r\circ q)(e, g)\cdot y(e,g) = [\phi_A(f) y(\cdot, g)] (e), \\
\end{align*}from which it follows that
 \begin{align*}
\mu^{(1)}(\Theta) y(e,g) - (\bar{\phi}_B|\circ \nu)(f) y(e,g) &= \Theta(y(\cdot, g))(e) - [\phi_A(f) y(\cdot, g)](e)\\
& = ([\Theta-\phi_A(f)]y(\cdot, g))(e).
\end{align*}
\begin{align*}
\mu^{(1)}(\Theta) y(e,g) - (\bar{\phi}_B|\circ \nu)(f) y(e,g) &= \Theta(y(\cdot, g))(e) - [\phi_A(f) y(\cdot, g)](e)\\
& = ([\Theta-\phi_A(f)]y(\cdot, g))(e).
\end{align*}So we compute
 \begin{align*}
&\|\mu^{(1)}(\Theta)-(\bar{\phi}_B|\circ \nu)(f)y\|^2\\
& = \sup_{F^0}\langle\mu^{(1)}(\Theta)-(\bar{\phi}_B|\circ \nu)(f)y, \mu^{(1)}(\Theta)-(\bar{\phi}_B|\circ \nu)(f)y\rangle(v, g)\\
& = \sup_{E^0, G}\langle(\Theta-\phi_A)(f)y(\cdot, g), (\Theta-\phi_A)(f)y(\cdot, g)\rangle(v)\\
& = \sup_G \|(\Theta-\phi_A)(f)y(\cdot, g)\|^2\\
& \leq \sup_G \|(\Theta-\phi_A)(f)\|^2\|y(\cdot, g)\|^2.\\
\end{align*}
\begin{align*}
&\|\mu^{(1)}(\Theta)-(\bar{\phi}_B|\circ \nu)(f)y\|^2\\
& = \sup_{F^0}\langle\mu^{(1)}(\Theta)-(\bar{\phi}_B|\circ \nu)(f)y, \mu^{(1)}(\Theta)-(\bar{\phi}_B|\circ \nu)(f)y\rangle(v, g)\\
& = \sup_{E^0, G}\langle(\Theta-\phi_A)(f)y(\cdot, g), (\Theta-\phi_A)(f)y(\cdot, g)\rangle(v)\\
& = \sup_G \|(\Theta-\phi_A)(f)y(\cdot, g)\|^2\\
& \leq \sup_G \|(\Theta-\phi_A)(f)\|^2\|y(\cdot, g)\|^2.\\
\end{align*}Taking square roots,
 \begin{align*}
&\left\|[\mu^{(1)}\circ \phi_A(f)]y-[\bar{\phi}_B|\circ\nu]y\right\|\\
&\leq\left\|[\mu^{(1)}\circ\phi_A(f)]y-\mu^{(1)}(\Theta)]y\right\|+\left\|\mu^{(1)}(\Theta)y-[\bar{\phi}_B|\circ \nu]y\right\|
\leq 2\epsilon\|y\|.
\end{align*}
\begin{align*}
&\left\|[\mu^{(1)}\circ \phi_A(f)]y-[\bar{\phi}_B|\circ\nu]y\right\|\\
&\leq\left\|[\mu^{(1)}\circ\phi_A(f)]y-\mu^{(1)}(\Theta)]y\right\|+\left\|\mu^{(1)}(\Theta)y-[\bar{\phi}_B|\circ \nu]y\right\|
\leq 2\epsilon\|y\|.
\end{align*} We can now show that ![]() $(\mu, \nu)$ is Cuntz–Pimsner covariant.
$(\mu, \nu)$ is Cuntz–Pimsner covariant.
Proof of Proposition 4.5
![]() $\nu$ is clearly non-degenerate, and Remark 10 shows that
$\nu$ is clearly non-degenerate, and Remark 10 shows that ![]() $\mu:X\to M_B(Y)$, satisfying the first two conditions. Lemmas 4.11 and 4.12 supply the next two conditions of Definition 5, so that
$\mu:X\to M_B(Y)$, satisfying the first two conditions. Lemmas 4.11 and 4.12 supply the next two conditions of Definition 5, so that ![]() $(\mu,\nu)$ is a Cuntz–Pimsner covariant correspondence homomorphism.
$(\mu,\nu)$ is a Cuntz–Pimsner covariant correspondence homomorphism.
The existence of ![]() $\Pi$ is now a consequence of [Reference Kaliszewski, Quigg and Robertson12, Corollary 3.6].
$\Pi$ is now a consequence of [Reference Kaliszewski, Quigg and Robertson12, Corollary 3.6].
Having completed the construction of ![]() $\Pi$ by Proposition 4.5, we return to the Diagram 4.1 and introduce the homomorphism
$\Pi$ by Proposition 4.5, we return to the Diagram 4.1 and introduce the homomorphism ![]() $\psi$. Since
$\psi$. Since ![]() $M(C^*(\mathcal{Q}\times_\kappa G))$ contains a copy of
$M(C^*(\mathcal{Q}\times_\kappa G))$ contains a copy of ![]() $M(C_0(F^0))$, we define
$M(C_0(F^0))$, we define ![]() $\psi:C_0(G)\to M(C_0(F^0))$ by
$\psi:C_0(G)\to M(C_0(F^0))$ by ![]() $\psi(\gamma)=\gamma\circ q_2$, where
$\psi(\gamma)=\gamma\circ q_2$, where ![]() $q_2$ is the projection of
$q_2$ is the projection of ![]() $F^0$ onto the second factor. Then the composition
$F^0$ onto the second factor. Then the composition ![]() $k_B\circ \psi:C_0(G)\to M(C^*(\mathcal{Q}\times_\kappa G))$ induces a coaction, which we denote by
$k_B\circ \psi:C_0(G)\to M(C^*(\mathcal{Q}\times_\kappa G))$ induces a coaction, which we denote by ![]() $\delta^{\psi}$.
$\delta^{\psi}$.
Proposition 4.13. The pair ![]() $(\Pi, k_B\circ\psi)$ is a covariant representation for the coaction
$(\Pi, k_B\circ\psi)$ is a covariant representation for the coaction ![]() $(C^*(\mathcal{Q}), \zeta)$ in
$(C^*(\mathcal{Q}), \zeta)$ in ![]() $M(C^*(\mathcal{Q}\times_\kappa G))$, so we have a unique integrated form
$M(C^*(\mathcal{Q}\times_\kappa G))$, so we have a unique integrated form ![]() $C^*(\mathcal{Q})\rtimes_\zeta G\to M(C^*(Q\times_\kappa G))$, which we will denote by
$C^*(\mathcal{Q})\rtimes_\zeta G\to M(C^*(Q\times_\kappa G))$, which we will denote by ![]() $\Pi\times\psi.$
$\Pi\times\psi.$
Proof. Our objective is to show that the diagram

commutes. Since ![]() $C^*(\mathcal{Q})$ is generated by the images of the canonical correspondence maps
$C^*(\mathcal{Q})$ is generated by the images of the canonical correspondence maps ![]() $(k_X, k_A)$, it is enough to confirm separately that
$(k_X, k_A)$, it is enough to confirm separately that
 \begin{align*}
\overline{\Pi\times \text{id}}\circ \zeta\circ k_A &= \delta^\psi\circ\Pi\circ k_A\\
\overline{\Pi\times \text{id}}\circ \zeta\circ k_X &= \delta^\psi\circ\Pi\circ k_X.\\
\end{align*}
\begin{align*}
\overline{\Pi\times \text{id}}\circ \zeta\circ k_A &= \delta^\psi\circ\Pi\circ k_A\\
\overline{\Pi\times \text{id}}\circ \zeta\circ k_X &= \delta^\psi\circ\Pi\circ k_X.\\
\end{align*}Beginning with the first computation, we witness
 \begin{align*}
\overline{\Pi\times \text{id}}\circ \zeta\circ k_A(a) &= \overline{\Pi\times\text{id}}\circ \overline{k_A\times\text{id}} (a\otimes 1) = \overline{\Pi\circ k_A\otimes\text{id}}(a\otimes 1)\\
&=\overline{k_B\circ\nu\otimes\text{id}}(a\otimes 1) = \overline{k_B\otimes \text{id}} (\nu(a)\otimes 1),
\end{align*}
\begin{align*}
\overline{\Pi\times \text{id}}\circ \zeta\circ k_A(a) &= \overline{\Pi\times\text{id}}\circ \overline{k_A\times\text{id}} (a\otimes 1) = \overline{\Pi\circ k_A\otimes\text{id}}(a\otimes 1)\\
&=\overline{k_B\circ\nu\otimes\text{id}}(a\otimes 1) = \overline{k_B\otimes \text{id}} (\nu(a)\otimes 1),
\end{align*} whose argument we identify as the operator valued function ![]() $\nu(a)\otimes 1\in C_b(F^0, M^\beta(C^* (G) ))$ assigning
$\nu(a)\otimes 1\in C_b(F^0, M^\beta(C^* (G) ))$ assigning ![]() $(v, g)\mapsto a(v)\iota(1)$. Attending to this argument
$(v, g)\mapsto a(v)\iota(1)$. Attending to this argument ![]() $\nu(a)\otimes 1$, we compute pointwise
$\nu(a)\otimes 1$, we compute pointwise
 \begin{align*}
\nu(a)\otimes1(v, g) &= a(v)\iota(1)= a(v)\iota(u_gu_g^*) = 1\otimes u_g\cdot a(v)\otimes 1\cdot 1\otimes u_g^*\\
&= [\overline{\psi\otimes\text{id}}(\omega_G)\cdot a\otimes1\cdot\overline{\psi\otimes\text{id}}(\omega_G)^*](v, g).
\end{align*}
\begin{align*}
\nu(a)\otimes1(v, g) &= a(v)\iota(1)= a(v)\iota(u_gu_g^*) = 1\otimes u_g\cdot a(v)\otimes 1\cdot 1\otimes u_g^*\\
&= [\overline{\psi\otimes\text{id}}(\omega_G)\cdot a\otimes1\cdot\overline{\psi\otimes\text{id}}(\omega_G)^*](v, g).
\end{align*} Then, since ![]() $\overline{k_B\otimes \text{id}}$ is a homomorphism, follows that
$\overline{k_B\otimes \text{id}}$ is a homomorphism, follows that ![]() $\overline{\Pi\times\text{id}}\circ \zeta\circ k_A = \delta^\psi\circ \Pi\circ k_A$.
$\overline{\Pi\times\text{id}}\circ \zeta\circ k_A = \delta^\psi\circ \Pi\circ k_A$.
We follow up with the second computation, which is a bit more delicate. Observe that
 \begin{align*}
&\delta^{\psi}\circ\Pi\circ k_X(x)\\
=&\delta^\psi\circ k_Y\circ\mu(x)\\
=&\overline{k_B\circ\psi\otimes\text{id}}(\omega_G)
\big(k_Y(\mu(x))\otimes1\big)
\overline{k_B\circ\psi\otimes\text{id}}(\omega_G)^*\\
=&\overline{k_B\otimes\text{id}}\circ\overline{\psi\otimes\text{id}}(\omega_G)
\big(k_Y(\mu(x))\otimes 1\big)
\overline{k_B\otimes\text{id}}\circ\overline{\psi\otimes\text{id}}(\omega_G)^*\\
=&\overline{k_B\otimes\text{id}}\circ\overline{\psi\otimes\text{id}}(\omega_G)
\big(\overline{k_Y\otimes\text{id}}(\mu(x)\otimes 1)\big)
\overline{k_B\otimes\text{id}}\circ\overline{\psi\otimes\text{id}}(\omega_G)^*\\
=&\overline{k_Y\otimes\text{id}}\Big[\overline{\psi\otimes\text{id}}(\omega_G)
\big(\mu(x)\otimes 1\big)
\overline{\psi\otimes\text{id}}(\omega_G)^*\Big],
\end{align*}
\begin{align*}
&\delta^{\psi}\circ\Pi\circ k_X(x)\\
=&\delta^\psi\circ k_Y\circ\mu(x)\\
=&\overline{k_B\circ\psi\otimes\text{id}}(\omega_G)
\big(k_Y(\mu(x))\otimes1\big)
\overline{k_B\circ\psi\otimes\text{id}}(\omega_G)^*\\
=&\overline{k_B\otimes\text{id}}\circ\overline{\psi\otimes\text{id}}(\omega_G)
\big(k_Y(\mu(x))\otimes 1\big)
\overline{k_B\otimes\text{id}}\circ\overline{\psi\otimes\text{id}}(\omega_G)^*\\
=&\overline{k_B\otimes\text{id}}\circ\overline{\psi\otimes\text{id}}(\omega_G)
\big(\overline{k_Y\otimes\text{id}}(\mu(x)\otimes 1)\big)
\overline{k_B\otimes\text{id}}\circ\overline{\psi\otimes\text{id}}(\omega_G)^*\\
=&\overline{k_Y\otimes\text{id}}\Big[\overline{\psi\otimes\text{id}}(\omega_G)
\big(\mu(x)\otimes 1\big)
\overline{\psi\otimes\text{id}}(\omega_G)^*\Big],
\end{align*} where the last line follows since ![]() $(k_Y, k_B)$ is a Toeplitz representation. Now, isolating the argument (which is a multiplier of
$(k_Y, k_B)$ is a Toeplitz representation. Now, isolating the argument (which is a multiplier of ![]() $Y\otimes C^* (G)$), we calculate pointwise for the elementary tensor
$Y\otimes C^* (G)$), we calculate pointwise for the elementary tensor ![]() $b\otimes\gamma\in B\otimes C^* (G)$
$b\otimes\gamma\in B\otimes C^* (G)$
 \begin{align*}
&\overline{\psi\otimes\text{id}}(\omega_G)(\mu(x)\otimes 1)\overline{\psi\otimes\text{id}}(\omega_G)^* (b\otimes\gamma)(e, g)\\
=&\overline{\psi\otimes\text{id}}(\omega_G)(r(e),\kappa(e)g)\cdot x(e)1\cdot\overline{\psi\otimes\text{id}}(\omega_G)^*(s(e), g) b(s(e), g)\gamma\\
=&u_{\kappa(e)g}\cdot x(e)1\cdot u_{g}^*\cdot b(s(e))\gamma\\
=&x(e)u_{\kappa(e)g}u_g^*\cdot b(s(e), g)\gamma\\
=&x(e)u_{\kappa(e)}\cdot b(s(e), g)\gamma\\
=&(v\cdot(x\otimes 1))\circ q(e, g)\cdot b\otimes\gamma(e, g)\\
=&\overline{\mu\otimes\text{id}}(v\cdot(x\otimes 1))(e, g)\cdot b\otimes\gamma(e, g).\\
\end{align*}
\begin{align*}
&\overline{\psi\otimes\text{id}}(\omega_G)(\mu(x)\otimes 1)\overline{\psi\otimes\text{id}}(\omega_G)^* (b\otimes\gamma)(e, g)\\
=&\overline{\psi\otimes\text{id}}(\omega_G)(r(e),\kappa(e)g)\cdot x(e)1\cdot\overline{\psi\otimes\text{id}}(\omega_G)^*(s(e), g) b(s(e), g)\gamma\\
=&u_{\kappa(e)g}\cdot x(e)1\cdot u_{g}^*\cdot b(s(e))\gamma\\
=&x(e)u_{\kappa(e)g}u_g^*\cdot b(s(e), g)\gamma\\
=&x(e)u_{\kappa(e)}\cdot b(s(e), g)\gamma\\
=&(v\cdot(x\otimes 1))\circ q(e, g)\cdot b\otimes\gamma(e, g)\\
=&\overline{\mu\otimes\text{id}}(v\cdot(x\otimes 1))(e, g)\cdot b\otimes\gamma(e, g).\\
\end{align*} Thus, the argument agrees with ![]() $\overline{\mu\otimes\text{id}}(v\cdot(x\otimes 1))$ on elementary tensors and consequently for all of
$\overline{\mu\otimes\text{id}}(v\cdot(x\otimes 1))$ on elementary tensors and consequently for all of ![]() $B\otimes C^* (G)$.
$B\otimes C^* (G)$.
With this in hand, we observe that
 \begin{align*}
&\delta^\psi\circ\Pi\circ k_X(x) \\
=& \overline{k_Y\otimes\text{id}}\left[\overline{\mu\otimes\text{id}}(v\cdot(x\otimes 1))\right] \\
=& \overline{k_Y\circ\mu\otimes\text{id}}(\sigma(x))\\
=&\overline{\Pi\circ k_X\otimes\text{id}}(\sigma(x)) \\
=& \overline{\Pi\otimes\text{id}}\circ\overline{k_X\otimes\text{id}}\circ\sigma(x) \\
=& \overline{\Pi\otimes\text{id}}\circ\zeta\circ k_X(x)\\
\end{align*}
\begin{align*}
&\delta^\psi\circ\Pi\circ k_X(x) \\
=& \overline{k_Y\otimes\text{id}}\left[\overline{\mu\otimes\text{id}}(v\cdot(x\otimes 1))\right] \\
=& \overline{k_Y\circ\mu\otimes\text{id}}(\sigma(x))\\
=&\overline{\Pi\circ k_X\otimes\text{id}}(\sigma(x)) \\
=& \overline{\Pi\otimes\text{id}}\circ\overline{k_X\otimes\text{id}}\circ\sigma(x) \\
=& \overline{\Pi\otimes\text{id}}\circ\zeta\circ k_X(x)\\
\end{align*} and we thus conclude that the pair ![]() $(\Pi, k_B\circ\psi)$ is a covariant representation of the coaction
$(\Pi, k_B\circ\psi)$ is a covariant representation of the coaction ![]() $(C^* (\mathcal{Q}), \zeta)$.
$(C^* (\mathcal{Q}), \zeta)$.
It remains for us to show that the integrated form ![]() $\Pi\times \psi$ is an isomorphism. We will show that the image of
$\Pi\times \psi$ is an isomorphism. We will show that the image of ![]() $\Pi\times\psi$ contains all of the generators of
$\Pi\times\psi$ contains all of the generators of ![]() $C^*(\mathcal{Q}\times_\kappa G)$ to deduce surjectivity and employ the Dual Invariant Uniqueness Theorem [Reference Huef, Quigg, Raeburn and Williams8, Theorem 5.4] to prove injectivity.
$C^*(\mathcal{Q}\times_\kappa G)$ to deduce surjectivity and employ the Dual Invariant Uniqueness Theorem [Reference Huef, Quigg, Raeburn and Williams8, Theorem 5.4] to prove injectivity.
Proposition 4.14. The map ![]() $\Pi\times \psi: C^*(\mathcal{Q})\times_\zeta G\to C^*(\mathcal{Q}\times_\kappa G)$ is surjective.
$\Pi\times \psi: C^*(\mathcal{Q})\times_\zeta G\to C^*(\mathcal{Q}\times_\kappa G)$ is surjective.
Proof. As stated above, we need only show that ![]() $\Pi\times\psi$ is surjective on the images of the generators
$\Pi\times\psi$ is surjective on the images of the generators ![]() $k_B(C_c(F^0)), k_Y(C_c(F^1))$. We check for
$k_B(C_c(F^0)), k_Y(C_c(F^1))$. We check for ![]() $a\in A$ and
$a\in A$ and ![]() $f\in C_0(G)$ that
$f\in C_0(G)$ that
 \begin{align*}
&\quad\Pi\times\psi(j_{C^*\mathcal{Q}}(k_A(a))j_G(f))\\
&= \Pi(k_A(a))k_B(\psi(f))\\
&= k_B(\nu(a))k_B(\psi(f)) = k_B(\nu(a)\psi(f))\\
&= k_B(a\otimes1\cdot 1\otimes f) = k_B(a\otimes f).
\end{align*}
\begin{align*}
&\quad\Pi\times\psi(j_{C^*\mathcal{Q}}(k_A(a))j_G(f))\\
&= \Pi(k_A(a))k_B(\psi(f))\\
&= k_B(\nu(a))k_B(\psi(f)) = k_B(\nu(a)\psi(f))\\
&= k_B(a\otimes1\cdot 1\otimes f) = k_B(a\otimes f).
\end{align*} A similar computation for ![]() $x\in C_c(E^1)$ shows
$x\in C_c(E^1)$ shows
 \begin{align*}
&\quad\Pi\times\psi(j_\mathcal{Q}(k_X(x))j_G(f))\\
&=\Pi(k_X(x))k_B(\psi(f))\\
&=k_Y(\mu(x))k_B(\psi(f))\\
&=k_Y(x\otimes1\cdot 1\otimes f)\\
&=k_Y(x\otimes f).
\end{align*}
\begin{align*}
&\quad\Pi\times\psi(j_\mathcal{Q}(k_X(x))j_G(f))\\
&=\Pi(k_X(x))k_B(\psi(f))\\
&=k_Y(\mu(x))k_B(\psi(f))\\
&=k_Y(x\otimes1\cdot 1\otimes f)\\
&=k_Y(x\otimes f).
\end{align*}Taking these equations together, we see that products such as
are contained in the image of ![]() $\Pi\times\psi.$ An argument in linearity and density now shows that the integrated form is surjective.
$\Pi\times\psi.$ An argument in linearity and density now shows that the integrated form is surjective.
Proposition 4.15. ![]() $\Pi\times\psi$ is injective.
$\Pi\times\psi$ is injective.
Proof. We apply [Reference Huef, Quigg, Raeburn and Williams8, Theorem 5.4]. First, this entails the covariant representation ![]() $(\Pi, \psi)$ in
$(\Pi, \psi)$ in ![]() $M(C^*(\mathcal{Q}\times_\kappa G))$ with
$M(C^*(\mathcal{Q}\times_\kappa G))$ with ![]() $\text{ker }\Pi=\text{ker }j_\mathcal{Q}$. Indeed, the gauge action on the skew product quiver intertwines the gauge action on
$\text{ker }\Pi=\text{ker }j_\mathcal{Q}$. Indeed, the gauge action on the skew product quiver intertwines the gauge action on ![]() $C^*(\mathcal{Q})$, so since
$C^*(\mathcal{Q})$, so since ![]() $\nu$ is injective, it follows that
$\nu$ is injective, it follows that ![]() $\Pi$ is injective. Then, since
$\Pi$ is injective. Then, since ![]() $\Pi=(\Pi\times\psi)\circ j_\mathcal{Q}$, it also follows that
$\Pi=(\Pi\times\psi)\circ j_\mathcal{Q}$, it also follows that ![]() $j_\mathcal{Q}$ is also injective, so that the kernels agree.
$j_\mathcal{Q}$ is also injective, so that the kernels agree.
Next, we need an action ![]() $\beta$ of
$\beta$ of ![]() $G$ on
$G$ on ![]() $C^*(\mathcal{Q}\times_\kappa G)$ whose strict extension fixes
$C^*(\mathcal{Q}\times_\kappa G)$ whose strict extension fixes ![]() $\Pi$ and acts by right translation on
$\Pi$ and acts by right translation on ![]() $\psi$. Define
$\psi$. Define ![]() $\beta_h$ as the action determined on
$\beta_h$ as the action determined on ![]() $C^*(\mathcal{Q}\times_\kappa G)$ by right translation on
$C^*(\mathcal{Q}\times_\kappa G)$ by right translation on ![]() $(Y, B)$. Then
$(Y, B)$. Then ![]() $\overline{\beta_h}(\Pi) = \Pi$, while
$\overline{\beta_h}(\Pi) = \Pi$, while ![]() $\overline{\beta_h}(\psi(f)) =\psi(\text{rt}_hf) $, satisfying the hypotheses of the theorem. It then follows that
$\overline{\beta_h}(\psi(f)) =\psi(\text{rt}_hf) $, satisfying the hypotheses of the theorem. It then follows that ![]() $\Pi\times\psi$ is injective.
$\Pi\times\psi$ is injective.
In the course of proving Proposition 4.15, we deduced an auxiliary result.
Corollary 4.16. The coaction ![]() $\zeta$ is normal.
$\zeta$ is normal.
Proof. In the proof above, we noticed that ![]() $j_{Q}$ is injective, which is the definition of normality of the coaction.
$j_{Q}$ is injective, which is the definition of normality of the coaction.
We are now prepared to prove the main theorem.
5. Application to duality
Topological quivers are quite abundant, as the following proposition shows.
Proposition 5.1. Suppose that ![]() $X, Y$ are two second countable locally compact Hausdorff spaces, and suppose that
$X, Y$ are two second countable locally compact Hausdorff spaces, and suppose that ![]() $f, g:X\to Y$ are both continuous maps. If
$f, g:X\to Y$ are both continuous maps. If ![]() $f$ is open and surjective, then there is a topological quiver with vertex space
$f$ is open and surjective, then there is a topological quiver with vertex space ![]() $Y$ and edge space
$Y$ and edge space ![]() $X$.
$X$.
Proof. This is an immediate consequence of Blanchard’s Theorem [Reference Blanchard2]. Since ![]() $f$ is an open and surjective map, there is an associated
$f$ is an open and surjective map, there is an associated ![]() $f$-system of probability measures
$f$-system of probability measures ![]() $\lambda=\{\lambda_y\}_{y\in Y}$. Then the ensemble
$\lambda=\{\lambda_y\}_{y\in Y}$. Then the ensemble ![]() $(Y, X, g, f, \lambda)$ is the desired topological quiver.
$(Y, X, g, f, \lambda)$ is the desired topological quiver.
In particular, topological quivers generalize directed graphs (where the spaces above are discrete), as well as topological graphs where the source map is a local homeomorphism. Theorem 4.3 thus recovers [Reference Kaliszewski, Quigg and Raeburn11, Theorem 2.4] as well as [Reference Kaliszewski and Quigg10, Theorem 3.1]. We mention that the approach used in this present article constructs the isomorphism ![]() $C^*\mathcal{Q}\times_\zeta G\cong C^*(\mathcal{Q}\times_\kappa G)$ with our bare hands, a departure from the technique of [Reference Kaliszewski and Quigg10] which employs Landstad duality to recover the coaction, then shows this coaction is equivalent to the constructed one. Presumably, this technique would work just as well.
$C^*\mathcal{Q}\times_\zeta G\cong C^*(\mathcal{Q}\times_\kappa G)$ with our bare hands, a departure from the technique of [Reference Kaliszewski and Quigg10] which employs Landstad duality to recover the coaction, then shows this coaction is equivalent to the constructed one. Presumably, this technique would work just as well.
We have shown that the coaction ![]() $\zeta$ associated with a cocycle on a topological quiver is injective and consequently a normal coaction. As mentioned in the preliminaries, it is possible for a coaction to be simultaneously normal and maximal, and Proposition 2.20 shows that this has strong implications for the dual action. So far, we have been unable to demonstrate the maximality of
$\zeta$ associated with a cocycle on a topological quiver is injective and consequently a normal coaction. As mentioned in the preliminaries, it is possible for a coaction to be simultaneously normal and maximal, and Proposition 2.20 shows that this has strong implications for the dual action. So far, we have been unable to demonstrate the maximality of ![]() $\zeta$, so we offer the claim here as a conjecture.
$\zeta$, so we offer the claim here as a conjecture.
Conjecture 5.2. If ![]() $\mathcal{Q}$ is a topological quiver equipped with a cocycle
$\mathcal{Q}$ is a topological quiver equipped with a cocycle ![]() $\kappa:E^1\to G$, over a locally compact group, then the natural coaction
$\kappa:E^1\to G$, over a locally compact group, then the natural coaction ![]() $\zeta$ described in Proposition 4.2 is maximal. Consequently, the regular representation in Proposition 2.20 is an isomorphism.
$\zeta$ described in Proposition 4.2 is maximal. Consequently, the regular representation in Proposition 2.20 is an isomorphism.
The conjecture holds trivially for amenable groups, and the analysis in [Reference Kaliszewski, Quigg and Raeburn11] shows that this holds for discrete groups and directed graphs without restriction. A positive answer to this question would generalize the work in the discrete setting and strengthen the results contained in [Reference Deaconu, Kumjian and Quigg3, Reference Kaliszewski and Quigg10]. As a final application, we deduce consequences for the ![]() ${C^*}$-algebra of a quiver which has a suitable principal action by a locally compact group.
${C^*}$-algebra of a quiver which has a suitable principal action by a locally compact group.
Corollary 5.3. Let ![]() $\mathcal{Q}$ is a topological quiver equipped with a free and proper action
$\mathcal{Q}$ is a topological quiver equipped with a free and proper action ![]() $\gamma$ by
$\gamma$ by ![]() $G$ for which the vertex orbit bundle
$G$ for which the vertex orbit bundle ![]() $(E^0, q, E^0/G)$ is trivial. If
$(E^0, q, E^0/G)$ is trivial. If ![]() $\alpha$ is the action on
$\alpha$ is the action on ![]() $C^*(\mathcal{Q})$ determined by the correspondence action
$C^*(\mathcal{Q})$ determined by the correspondence action ![]() $g\cdot \xi(e) = \xi(\gamma_g(e))$ and
$g\cdot \xi(e) = \xi(\gamma_g(e))$ and ![]() $g\cdot f(v) = (\gamma_g(v))$, then
$g\cdot f(v) = (\gamma_g(v))$, then
Consequently, the reduced crossed product is Morita equivalent to the ![]() ${C^*}$-algebra of the quotient quiver.
${C^*}$-algebra of the quotient quiver.
Proof. Write ![]() $\mathcal{R} = q(\mathcal{Q})$ for the quotient quiver under the action. According to Theorem 3.8,
$\mathcal{R} = q(\mathcal{Q})$ for the quotient quiver under the action. According to Theorem 3.8, ![]() $\mathcal{Q}$ is a skew product quiver
$\mathcal{Q}$ is a skew product quiver ![]() $\mathcal{R}\times_\kappa G$, so
$\mathcal{R}\times_\kappa G$, so ![]() $C^*(\mathcal{Q}) = C^*(\mathcal{R}\times_\kappa G)$ is G-equivariantly isomorphic to
$C^*(\mathcal{Q}) = C^*(\mathcal{R}\times_\kappa G)$ is G-equivariantly isomorphic to ![]() $C^*(\mathcal{R})\times_\zeta G$ for the natural coaction
$C^*(\mathcal{R})\times_\zeta G$ for the natural coaction ![]() $\zeta$. Since
$\zeta$. Since ![]() $\zeta$ is a normal coaction (see Corollary 2), Katayama duality applies [Reference Echterhoff, Kaliszewski, Quigg and Raeburn4.16, Theorem A.69] and
$\zeta$ is a normal coaction (see Corollary 2), Katayama duality applies [Reference Echterhoff, Kaliszewski, Quigg and Raeburn4.16, Theorem A.69] and
Acknowledgements
The author would like to thank John Quigg for numerous discussions and insights regarding this work. Without his patient encouragement and diligent guidance, this work would be far inferior.
Competing interests
The author declares none.