Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T10:15:58.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of Symmetric Special Biserial Algebras With At Most One Non-Uniserial Indecomposable Projective

Published online by Cambridge University Press:  13 February 2015

Nicole Snashall  and
Rachel Taillefer
Nicole Snashall
Affiliation:
Department of Mathematics, University of Leicester, University Road, Leicester LE1 7RH, UK ([email protected])
Rachel Taillefer
Affiliation:
Laboratoire de Mathématiques, UMR 6620, Université Blaise Pascal, Complexe Universitaire des Cézeaux, 63171 Aubière, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a natural generalization of symmetric Nakayama algebras, namely, symmetric special biserial algebras with at most one non-uniserial indecomposable projective module. We describe the basic algebras explicitly by quiver and relations, then classify them up to derived equivalence and up to stable equivalence of Morita type. This includes the weakly symmetric algebras of Euclidean type 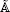n, as studied by Bocian et al., as well as some algebras of dihedral type.

Keywords

special biserial algebraderived equivalencestable equivalence of Morita typegeneralized Brauer tree algebraPrimary 16D5016E35Secondary 16E40
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 3 , October 2015 , pp. 739 - 767
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Al-Nofayee, S., Equivalences of derived categories for self-injective algebras, J. Alg. 313(2 (2007), 897–904.CrossRefGoogle Scholar
2.Alperin, J. L., Local representation theory: modular representations as an introduction to the local representation theory of finite groups, Cambridge Studies in Advanced Mathematics, Volume 11 (Cambridge University Press, 1986).Google Scholar
3.Antipov, M. A. and Generalov, A. I., The Yoneda algebras of symmetric special biserial algebras are finitely generated, St Petersburg Math. J. 17(3 (2006), 377–392.Google Scholar
4.Benson, D., Representations and cohomology, I: basic representation theory of finite groups and associative algebras, Cambridge Studies in Advanced Mathematics, Volume 30 (Cambridge University Press, 1991).Google Scholar
5.Bocian, R. and Skowroński, A., Weakly symmetric algebras of Euclidean type, J. Reine Angew. Math. 580 (2005), 157–199.CrossRefGoogle Scholar
6.Bocian, R., Holm, T. and Skowroński, A., Derived equivalence classification of weakly symmetric algebras of Euclidean type, J. Pure Appl. Alg. 191(1–2) (2004), 43–74.CrossRefGoogle Scholar
7.Erdmann, K., Blocks of tame representation type and related algebras, Springer Lecture Notes in Mathematics, Volume 1428 (Springer, 1990).CrossRefGoogle Scholar
8.Gabriel, P. and Riedtmann, Ch., Group representations without groups, Comment. Math. Helv. 54(2 (1979), 240–287.Google Scholar
9.Green, E. L. and Snashall, N., Projective bimodule resolutions of an algebra and vanishing of the second Hochschild cohomology group, Forum Math. 16(1 (2004), 17–36.CrossRefGoogle Scholar
10.Happel, D., Hochschild cohomology of finite-dimensional algebras, in Séminaire d’Algèbre Paul Dubreil et Marie-Paul Malliavin, Lecture Notes in Mathematics, Volume 1404, pp. 108–126 (Springer, 1989).CrossRefGoogle Scholar
11.Holm, T., Derived equivalent tame blocks, J. Alg. 194 (1997), 178–200.Google Scholar
12.Holm, T., Derived equivalence classification of algebras of dihedral, semidihedral, and quaternion type, J. Alg. 211(1 (1999), 159–205.CrossRefGoogle Scholar
13.Holm, T. and Zimmermann, A., Generalized Reynolds ideals and derived equivalences for algebras of dihedral and semidihedral type, J. Alg. 320(9 (2008), 3425–3437.CrossRefGoogle Scholar
14.Kauer, M., Derived equivalence of graph algebras, in Trends in the representation theory of finite dimensional algebras, Contemporary Mathematics, Volume 229, pp. 201–213 (American Mathematical Society, Providence, RI, 1998).CrossRefGoogle Scholar
15.Keller, B. and Vossieck, D., Sous les catégories dérivées, C. R. Acad. Sci. Paris I 305(6 (1987), 225–228.Google Scholar
16.Koenig, S., Liu, Y. and Zhou, G., Transfer maps in Hochschild (co)homology and applications to stable and derived invariants and to the Auslander-Reiten conjecture, Trans. Am. Math. Soc. 364(1 (2012), 195–232.CrossRefGoogle Scholar
17.Linckelmann, M., A derived equivalence for blocks with dihedral defect groups, J. Alg. 164 (1994), 244–255.Google Scholar
18.Liu, Y., Summands of stable equivalences of Morita type, Commun. Alg. 36 (2008), 3778–3782.Google Scholar
19.Liu, Y., Zhou, G. and Zimmermann, A., Higman ideal, stable Hochschild homology and Auslander-Reiten conjecture, Math. Z. 270(3–4) (2012), 759–781.Google Scholar
20.Membrillo-Hernández, F. H., Brauer tree algebras and derived equivalence, J. Pure Appl. Alg. 114(3 (1997), 231–258.CrossRefGoogle Scholar
21.Pogorzaly, Z., Algebras stably equivalent to self-injective special biserial algebras, Commun. Alg. 22(4 (1994), 1127–1160.CrossRefGoogle Scholar
22.Rickard, J., Derived categories and stable equivalence, J. Pure Appl. Alg. 61(3 (1989), 303–317.CrossRefGoogle Scholar
23.Rickard, J., Derived equivalences as derived functors, J. Lond. Math. Soc. 43 (1991), 37–48.CrossRefGoogle Scholar
24.Roggenkamp, K. W., Biserial algebras and graphs, in Algebras and modules II, Conference Proceedings, Canadian Mathematical Society, Volume 24, pp. 481–496 (American Mathematical Society, Providence, RI, 1998).Google Scholar
25.Skowroński, A., Selfinjective algebras: finite and tame type, in Trends in representation theory of algebras and related topics, Contemporary Mathematics, Volume 406, pp. 169–238 (American Mathematical Society, Providence, RI, 2006).Google Scholar
26.Snashall, N. and Taillefer, R., The Hochschild cohomology ring of a class of special biserial algebras, J. Alg. Appl. 9(1 (2010), 73–122.CrossRefGoogle Scholar
27.Wald, B. and Waschbüsch, J., Tame biserial algebras, J. Alg. 95(2 (1985), 480–500.CrossRefGoogle Scholar
28.Xi, C., Stable equivalences of adjoint type, Forum Math. 20(1 (2008), 81–97.Google Scholar
29.Zimmermann, A., Invariance of generalized Reynolds ideals under derived equivalences, Math. Proc. R. Irish Acad. A 107(1 (2007), 1–9.CrossRefGoogle Scholar