Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-08T19:29:40.554Z Has data issue: false hasContentIssue false
  • English
  • Français

A class of simple non-weight modules over the virasoro algebra

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  07 August 2020

Haibo Chen  and
JianZhi Han
Haibo Chen
Affiliation:
School of Statistics and Mathematics, Shanghai Lixin University of Accounting and Finance, Shanghai201209, China ([email protected])
JianZhi Han
Affiliation:
School of Mathematical Sciences, Tongji University, Shanghai200092, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The Virasoro algebra $\mathcal {L}$ is an infinite-dimensional Lie algebra with basis {Lm, C| m ∈ ℤ} and relations [Lm, Ln] = (n − m)Lm+n + δm+n,0((m3 − m)/12)C, [Lm, C] = 0 for m, n ∈ ℤ. Let 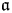$\mathfrak a$ be the subalgebra of 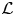$\mathcal {L}$ spanned by Li for i ≥ −1. For any triple (μ, λ, α) of complex numbers with μ ≠ 0, λ ≠ 0 and any non-trivial 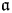$\mathfrak a$-module V satisfying the condition: for any v ∈ V there exists a non-negative integer m such that Liv = 0 for all i ≥ m, non-weight 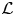$\mathcal {L}$-modules on the linear tensor product of V and ℂ[∂], denoted by 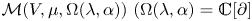$\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))\ (\Omega (\lambda ,\alpha )=\mathbb {C}[\partial ]$ as vector spaces), are constructed in this paper. We prove that 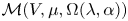$\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))$ is simple if and only if μ ≠ 1, λ ≠ 0, α ≠ 0. We also give necessary and sufficient conditions for two such simple 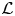$\mathcal {L}$-modules being isomorphic. Finally, these simple 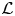$\mathcal {L}$-modules 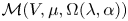$\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))$ are proved to be new for V not being the highest weight 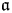$\mathfrak a$-module whose highest weight is non-zero.

Keywords

Virasoro algebranon-weight modulesimple module

MSC classification

Primary: 17B10: Representations, algebraic theory (weights)
Secondary: 17B65: Infinite-dimensional Lie (super)algebras 17B68: Virasoro and related algebras
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 4 , November 2020 , pp. 956 - 970
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Block, R. E., The irreducible representations of the Lie algebra $\mathfrak {sl}(2)$ and of the Weyl algebra, Adv. Math. 139 (1981), 69–110.CrossRefGoogle Scholar
Chen, H. and Guo, X., A new family of modules over the Virasoro algebra, J. Algebra 457 (2016), 73–105.CrossRefGoogle Scholar
Chen, H. and Guo, X., Non-weight modules over the Heisenberg-Virasoro algebra and the W algebra W(2, 2), J. Algebra Appl. 16 (2017), 1750097.CrossRefGoogle Scholar
Chen, H., Guo, X. and Zhao, K., Tensor product weight modules over the Virasoro algebra, J. Lond. Math. Soc. 88 (2013), 829–844.CrossRefGoogle Scholar
Conley, C. H. and Martin, C., A family of irreducible representations of the Witt Lie algebra with infinite-dimensional weight spaces, Compositio Math. 128 (2001), 153–175.CrossRefGoogle Scholar
Guo, X., Lü, R. and Zhao, K., Fraction representations and highest weight-like representations of the Virasoro algebra, J. Algebra 387 (2013), 68–86.CrossRefGoogle Scholar
Han, J. and Su, Y., Submodule structure of ℂ[s, t] over W(0, b) and a new class of irreducible modules over the Virasoro algebra, arXiv:1708.07272.Google Scholar
Iohara, K. and Koga, Y., Representation theory of the Virasoro algebra, Springer Monographs in Mathematics (Springer, London, 2011).CrossRefGoogle Scholar
Kac, V. G. and Raina, A. K., Bombay Lectures on Highest Weight Representations of Infinite-dimensional Lie Algebras, Volume 2 (World Scientific Publishing, Teaneck, 1987).Google Scholar
Liu, D. and Jiang, C., Harish-Chandra modules over the twisted Heisenberg-Virasoro algebra, J. Math. Phys. 49 (2008), 012901, 13 p.CrossRefGoogle Scholar
Liu, G. and Zhao, Y., Generalized polynomial modules over the Virasoro algebra, Proc. Amer. Math. Soc. 144 (2016), 5103–5112.CrossRefGoogle Scholar
Liu, G., Lü, R. and Zhao, K., A class of simple weight Virasoro modules, J. Algebra 424 (2015), 506–521.CrossRefGoogle Scholar
Liu, X., Guo, X. and Wang, J., A new class of irreducible Virasoro modules from tensor product, J. Algebra 541 (2020), 324–344.CrossRefGoogle Scholar
Lü, R. and Zhao, K., Irreducible Virasoro modules from irreducible Weyl modules, J. Algebra 414 (2014), 271–287.CrossRefGoogle Scholar
Lü, R. and Zhao, K., A family of simple weight Virasoro modules, J. Algebra 479 (2017), 437–460.CrossRefGoogle Scholar
Lü, R., Guo, X. and Zhao, K., Irreducible modules over the Virasoro algebra, Doc. Math. 16 (2011), 709–721.Google Scholar
Mathieu, O., Classification of Harish-Chandra modules over the Virasoro Lie algebra, Invent. Math. 107 (1992), 225–234.CrossRefGoogle Scholar
Mazorchuk, V. and Wiesner, E., Simple Virasoro modules induced from codimension one subalgebras of the positive part, Proc. Amer. Math. Soc. 142 (2014), 3695–3703.CrossRefGoogle Scholar
Mazorchuk, V. and Zhao, K., Classification of simple weight Virasoro modules with a finite-dimensional weight space, J. Algebra 307 (2007), 209–214.CrossRefGoogle Scholar
Mazorchuk, V. and Zhao, K., Simple Virasoro modules which are locally finite over a positive part, Selecta Math. (N. S.) 20 (2014), 839–854.CrossRefGoogle Scholar
Ondrus, M. and Wiesner, E., Whittaker modules for the Virasoro algebra, J. Algebra Appl. 8 (2009), 363–377.CrossRefGoogle Scholar
Tan, H. and Zhao, K., Irreducible Virasoro modules from tensor products II, J. Algebra 394 (2013), 357–373.CrossRefGoogle Scholar
Tan, H. and Zhao, K., Irreducible Virasoro modules from tensor products, Ark. Mat. 54 (2016), 181–200.CrossRefGoogle Scholar
Zhang, H., A class of representations over the Virasoro algebra, J. Algebra 190 (1997), 1–10.CrossRefGoogle Scholar