Article contents
A characterisation of a certain class of convolution algebras
Published online by Cambridge University Press: 20 January 2009
Extract
In (6) Taylor has introduced the notion of a convolution measure algebra. In the same paper he constructed a canonical embedding of an arbitrary, semisimple commutative convolution measure algebra A into the algebra M(S) of all bounded, regular Borel measures on a compact semigroup S. This embedding has the properties that A is σ(M(S), C(S)-dense in M(S), that if μ is in A and ν is absolutely continuous with respect to μ, then ν is in A and that the set A^ of non-zero complex homomorphisms of A can be identified with the set S^ of continuous semicharacters of S where h ∈ A^ is identified with χ ∈ S^ by the equation
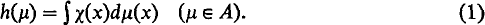
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1973
- 1
- Cited by


