Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T15:01:42.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Brauer indecomposability of Scott modules with semidihedral vertex

Part of: Representation theory of groups

Published online by Cambridge University Press:  04 May 2021

Shigeo Koshitani  and
İpek Tuvay
Shigeo Koshitani
Affiliation:
Center for Frontier Science, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba263-8522, Japan ([email protected])
İpek Tuvay
Affiliation:
Department of Mathematics, Mimar Sinan Fine Arts University, Bomonti, Şişli, Istanbul34380, Turkey ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a sufficient condition for the $kG$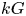-Scott module with vertex $P$ 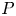to remain indecomposable under the Brauer construction for any subgroup $Q$ 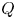of $P$ 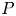as $k[Q\,C_G(Q)]$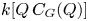-module, where $k$ 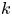is a field of characteristic $2$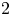, and $P$ 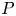is a semidihedral $2$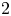-subgroup of a finite group $G$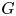. This generalizes results for the cases where $P$ 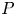is abelian or dihedral. The Brauer indecomposability is defined by R. Kessar, N. Kunugi and N. Mitsuhashi. The motivation of this paper is the fact that the Brauer indecomposability of a $p$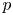-permutation bimodule (where $p$ 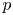is a prime) is one of the key steps in order to obtain a splendid stable equivalence of Morita type by making use of the gluing method due to Broué, Rickard, Linckelmann and Rouquier, that then can possibly be lifted to a splendid derived (splendid Morita) equivalence.

Keywords

Brauer indecomposabilityScott moduleBrauer constructionsemidihedral group

MSC classification

Primary: 20C20: Modular representations and characters
Secondary: 20C05: Group rings of finite groups and their modules 20C15: Ordinary representations and characters
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 174 - 182
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aschbacher, M., Kessar, R. and Oliver, B., Fusion systems in algebra and topology, London Math. Soc. Lecture Note Series, Volume 391 (Cambridge University Press, Cambridge, 2011).10.1017/CBO9781139003841CrossRefGoogle Scholar
Brauer, R., Some applications of the theory of blocks of characters of finite groups III, J. Algebra 3 (1966), 225–255.CrossRefGoogle Scholar
Broto, C., Levi, R. and Oliver, B., The homotopy theory of fusion systems, J. Am. Math. Soc. 16 (2003), 779–856.CrossRefGoogle Scholar
Broué, M., Equivalences of blocks of group algebras, in Finite-dimensional algebras and related topics (Ottawa 1992) (eds. V. Dlab and L. L. Scott), pp. 1–26 (Kluwer Academic Pub., Dordrecht, 1994).CrossRefGoogle Scholar
Broué, M., On Scott modules and $p$-permutation modules: an approach through the Brauer morphism, Proc. Am. Math. Soc. 93 (1985), 401–408.10.2307/2045600CrossRefGoogle Scholar
Broué, M. and Puig, L., Characters and local structure in $G$-algebras, J. Algebra 63 (1980), 306–317.CrossRefGoogle Scholar
Craven, D. and Glesser, A., Fusion systems on small $p$-groups, Trans. Am. Math. Soc. 364 (2012), 5945–5967.10.1090/S0002-9947-2012-05580-2CrossRefGoogle Scholar
Gorenstein, D., Finite groups (New York, Harper and Row, 1968).Google Scholar
Ishioka, H. and Kunugi, N., Brauer indecomposability of Scott modules, J. Algebra 470 (2017), 441–449.CrossRefGoogle Scholar
Kawai, H., On indecomposable modules and blocks, Osaka J. Math. 23 (1986), 201–205.Google Scholar
Kessar, R., Kunugi, N. and Mitsuhashi, N., On saturated fusion systems and Brauer indecomposability of Scott modules, J. Algebra 340 (2011), 90–103.CrossRefGoogle Scholar
Kessar, R., Koshitani, S. and Linckelmann, M., On the Brauer indecomposability of Scott modules, Quarterly J. Math. 66 (2015), 895–903.CrossRefGoogle Scholar
Koshitani, S. and Lassueur, C., Splendid Morita equivalences for principal 2-blocks with dihedral defect groups, Math. Z. 294 (2020), 639–666.CrossRefGoogle Scholar
Koshitani, S. and Lassueur, C., Splendid Morita equivalences for principal 2-blocks with generalised quaternion defect groups, J. Algebra 558 (2020), 523–533.CrossRefGoogle Scholar
Koshitani, S. and Tuvay, İ., The Brauer indecomposability of Scott modules for the quadratic group Qd($p$), Algebr. Represent. Theory 22 (2019), 1387–1397.CrossRefGoogle Scholar
Kwon, T., Lee, K., Cho, I. and Park, S., On finite groups with quasi-dihedral Sylow 2-groups, J. Korean Math. Soc. 17 (1980), 91–97.Google Scholar
Linckelmann, M., Introduction to fusion systems, in Group representation theory (Lausanne 2006) (eds. M. Geck, D. Testerman, and J. Thévenaz), pp. 79–113 (EPFL Press, Lausanne, 2007)Google Scholar
Nagao, H. and Tsushima, Y., Representations of finite groups (New York, Academic Press, 1989).Google Scholar
Olsson, J. B., On $2$-blocks with quaternion and quasidihedral defect groups, J. Algebra 36 (1975), 212–241.CrossRefGoogle Scholar
Thévenaz, J., G-algebras and modular representation theory (Oxford, Clarendon Press, 1995).Google Scholar
Tuvay, İ., On Brauer indecomposability of Scott modules of Park-type groups, J. Group Theory 17 (2014), 1071–1079.CrossRefGoogle Scholar