Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T08:52:13.438Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounding size of homotopy groups of Spheres

Part of: Homotopy groups

Published online by Cambridge University Press:  05 November 2020

Guy Boyde
Guy Boyde*
Affiliation:
Mathematical Sciences, University of Southampton, SouthamptonSO17 1BJ, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let p be prime. We prove that, for n odd, the p-torsion part of πq(Sn) has cardinality at most $p^{2^{{1}/({p-1})(q-n+3-2p)}}$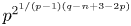 and hence has rank at most 21/(p−1)(q−n+3−2p). for p = 2, these results also hold for n even. The best bounds proven in the existing literature are $p^{2^{q-n+1}}$ 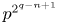and 2q−n+1, respectively, both due to Hans–Werner Henn. The main point of our result is therefore that the bound grows more slowly for larger primes. As a corollary of work of Henn, we obtain a similar result for the homotopy groups of a broader class of spaces.

Keywords

homotopy groups of spheresEHP sequence

MSC classification

Primary: 55Q40: Homotopy groups of spheres
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 4 , November 2020 , pp. 1100 - 1105
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bödigheimer, C.-F. and Henn, H.-W., A remark on the size of πq(Sn), Manuscripta Math. 42(1) (1983), 79–83.CrossRefGoogle Scholar
Flajolet, P. and Prodinger, H., Level number sequences for trees, Discrete Math. 65(2) (1987), 149–156.CrossRefGoogle Scholar
Henn, H.-W., On the growth of homotopy groups, Manuscripta Math. 56(2) (1986), 235–245.CrossRefGoogle Scholar
Husemoller, D., Fibre bundles, 3rd ed., Graduate Texts in Mathematics, Vol. 20 (Springer-Verlag, New York, 1994).CrossRefGoogle Scholar
Iriye, K., On the ranks of homotopy groups of a space, Publ. Res. Inst. Math. Sci. 23(1) (1987), 209–213.CrossRefGoogle Scholar
James, I. M., On the suspension sequence, Ann. Math. 65(2) (1957), 74–107.CrossRefGoogle Scholar
Selick, P., A bound on the rank of πq(S n), Illinois J. Math. 26(2) (1982), 293–295.CrossRefGoogle Scholar
Serre, J.-P., Homologie singulière des espaces fibrés, Appl. Ann. Math. 54(2) (1951), 425–505.Google Scholar
Serre, J.-P., Groupes d'homotopie et classes de groupes abéliens, Ann. of Math. 58(2) (1953), 258–294.CrossRefGoogle Scholar
Toda, H., On the double suspension E 2, J. Inst. Polytech. Osaka City Univ. Ser. A. 7 (1956), 103–145.Google Scholar