Article contents
A boundary value problem on an infinite interval
Published online by Cambridge University Press: 20 January 2009
Extract
We are interested here in proving the existence of solutions to the (generalised) boundary value problem

where A is a continuous n×n matrix on R+ = [0, ∞), F is a continuous n vector on R+ × S (S = a suitable subset of Rn), T is a bounded linear operator defined on (or on a subspace of) C[R+, Rn], the space of all bounded and continuous Rn-valued functions on R+, and r is a fixed vector in Rn. There is an abundance of papers dealing with the problem ((I), (II)) on finite intervals, either in its full generality (cf., for example, (1), (2), (3), (4), (6)), or for special cases of the operator T. The reader is especially referred to the work of Shreve (7), (8) for such problems on infinite intervals for scalar equations. A series representation of the solutions is given by Kravchenko and Yablonskii (5). Most of our methods are extensions of the corresponding ones on finite intervals with some variations concerning the application of fixed-point theorems. Examples of interesting operators T are
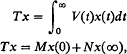
where V(t), M, N are n×n matrices with V(t) integrable.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 3 , March 1975 , pp. 245 - 252
- Copyright
- Copyright © Edinburgh Mathematical Society 1975
References
REFERENCES
- 11
- Cited by


