Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T20:40:02.816Z Has data issue: false hasContentIssue false
  • English
  • Français

Bootstrapping partition regularity of linear systems

Part of: Extremal combinatorics

Published online by Cambridge University Press:  09 March 2020

Tom Sanders
Tom Sanders*
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that A is a k × d matrix of integers and write 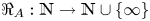$\Re _A:{\mathbb N}\to {\mathbb N}\cup \{ \infty \} $ for the function taking r to the largest N such that there is an r-colouring 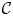$\mathcal {C}$ of [N] with 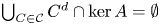$\bigcup _{C \in \mathcal {C}}{C^d}\cap \ker A =\emptyset $. We show that if ℜA(r) < ∞ for all 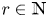$r\in {\mathbb N}$ then 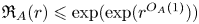$\mathfrak {R}_A(r) \leqslant \exp (\exp (r^{O_{A}(1)}))$ for all r ⩾ 2. When the kernel of A consists only of Brauer configurations – that is, vectors of the form (y, x, x + y, …, x + (d − 2)y) – the above statement has been proved by Chapman and Prendiville with good bounds on the OA(1) term.

Keywords

colouringRado numbersGowers uniformity

MSC classification

Primary: 05D10: Ramsey theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 3 , August 2020 , pp. 630 - 653
Check for updates
Copyright
Copyright © Edinburgh Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Abbott, H. L. and Moser, L., Sum-free sets of integers, Acta Arith. 11 (1966), 393–396.Google Scholar
2.Ahmed, T. and Schaal, D. J., On generalized Schur numbers, Exp. Math. 25(2) (2016), 213–218.CrossRefGoogle Scholar
3.Beutelspacher, A. and Brestovansky, W., Generalized Schur numbers, in Combinatorial theory (Schloss Rauischholzhausen, 1982) (eds Jungnickel, D. and Vedder, K.), pp. 30–38, Lecture Notes in Mathematics, Volume 969 (Springer, Berlin, 1982).CrossRefGoogle Scholar
4.Bourgain, J., On triples in arithmetic progression, Geom. Funct. Anal. 9(5) (1999), 968–984.CrossRefGoogle Scholar
5.Chapman, J., Partition regularity and multiplicatively syndetic sets, preprints (arXiv.org/abs/1902.01149, 2019).Google Scholar
6.Chapman, J. and Prendiville, S., On the Ramsey number of the Brauer configuration, preprint (arXiv.org/abs/1904.07567v1, 2019).Google Scholar
7.Chow, S., Lindqvist, S. and Prendiville, S., Rado's criterion over squares and higher powers, preprint (arXiv.org/abs/1806.05002, 2018).Google Scholar
8.Cwalina, K. and Schoen, T., Tight bounds on additive Ramsey-type numbers, J. Lond. Math. Soc. 96(3) (2017), 601–620.CrossRefGoogle Scholar
9.Deuber, W., Partitionen und lineare Gleichungssysteme, Math. Z. 133 (1973), 109–123.CrossRefGoogle Scholar
10.Frankl, P., Graham, R. L. and Rödl, V., Quantitative theorems for regular systems of equations, J. Combin. Theory Ser. A 47(2) (1988), 246–261.CrossRefGoogle Scholar
11.Gasarch, W., Moriarty, R. and Tumma, N., New upper and lower bounds on the Rado numbers, preprint (arXiv.org/abs/1206.4885, 2012).Google Scholar
12.Gowers, W. T., A new proof of Szemerédi's theorem for arithmetic progressions of length four, Geom. Funct. Anal. 8(3) (1998), 529–551.CrossRefGoogle Scholar
13.Gowers, W. T., A new proof of Szemerédi's theorem, Geom. Funct. Anal. 11(3) (2001), 465–588.CrossRefGoogle Scholar
14.Gowers, W. T. and Wolf, J., The true complexity of a system of linear equations, Proc. Lond. Math. Soc. (3) 100(1) (2010), 155–176.CrossRefGoogle Scholar
15.Graham, R. L. and Rothschild, B. L., Ramsey's theorem for n-parameter sets, Trans. Amer. Math. Soc. 159 (1971), 257–292.Google Scholar
16.Graham, R. L., Rothschild, B. L. and Spencer, J. H., Ramsey theory, 2nd edn, Wiley-Interscience Series in Discrete Mathematics and Optimization (John Wiley & Sons, New York, 1990).Google Scholar
17.Green, B. J., Finite field models in additive combinatorics, in Surveys in combinatorics 2005, pp. 1–27, London Mathematical Society Lecture Note Series, Volume 327 (Cambridge University Press, Cambridge, 2005).Google Scholar
18.Green, B. J. and Lindqvist, S., Monochromatic solutions to x + y = z 2, Can. J. Math. 71(3) (2019), 579–605.CrossRefGoogle Scholar
19.Green, B. J. and Sanders, T., Monochromatic sums and products, Discrete Anal. (5) (arXiv:1510.08733, 2016). doi:10.19086/da.613.Google Scholar
20.Green, B. J. and Tao, T. C., An arithmetic regularity lemma, an associated counting lemma, and applications, in An irregular mind, pp. 261–334, Bolyai Society Mathematical Studies, Volume 21 (János Bolyai Mathematical Society, Budapest, 2010).CrossRefGoogle Scholar
21.Green, B. J. and Tao, T. C., Linear equations in primes, Ann. Math. (2) 171(3) (2010), 1753–1850.CrossRefGoogle Scholar
22.Gunderson, D. S., On Deuber's partition theorem for (m, p, c)-sets, Ars Combin. 63 (2002), 15–31.Google Scholar
23.Gupta, S., Thulasi Rangan, J. and Tripathi, A., The two-colour Rado number for the equation ax + by = (a + b)z, Ann. Comb. 19(2) (2015), 269–291.CrossRefGoogle Scholar
24.Hatami, H. and Lovett, S., Higher-order Fourier analysis of $\mathbb {F}^n_p$ and the complexity of systems of linear forms, Geom. Funct. Anal. 21(6) (2011), 1331–1357.CrossRefGoogle Scholar
25.Hindman, N. and Leader, I. B., Nonconstant monochromatic solutions to systems of linear equations, in Topics in discrete mathematics, pp. 145–154, Algorithms and Combinatorics, Volume 26 (Springer, Berlin, 2006).CrossRefGoogle Scholar
26.Landman, B. M. and Robertson, A., Ramsey theory on the integers, 2nd edn, Student Mathematical Library, Volume 73 (American Mathematical Society, Providence, RI, 2014).Google Scholar
27.Lê, T. H., Partition regularity and the primes, C. R. Math. 350(9) (2012), 439–441.CrossRefGoogle Scholar
28.Li, H. and Pan, H., A Schur-type addition theorem for primes, J. Number Theory 132(1) (2012), 117–126.CrossRefGoogle Scholar
29.Manners, F., Good bounds in certain systems of true complexity one, Discrete Anal. (21) (arXiv:1705.06801, 2018). doi:10.19086/da.6814.Google Scholar
30.Prendiville, S., Quantitative bounds in the polynomial Szemerédi theorem: the homogeneous case, Discrete Anal. 5 (2017), 1–34.Google Scholar
31.Rado, R., Studien zur Kombinatorik, Math. Z. 36 (1933), 424–480.CrossRefGoogle Scholar
32.Rado, R., Some partition theorems, in Combinatorial theory and its applications, III, Proc. Colloq., Balatonfüred, 1969, pp. 929–936 (János Bolyai Mathematical Society, 1970).Google Scholar
33.Robertson, A. and Myers, K., Some two color, four variable Rado numbers, Adv. Appl. Math. 41(2) (2008), 214–226.CrossRefGoogle Scholar
34.Sanders, J. H., A generalization of Schur's theorem. PhD thesis, Yale University, 1968. http://gateway.proquest.com/openurl?url_ver=Z39.88-2004&rft_val_fmt=info:ofi/fmt:kev:mtx:dissertation&res_dat=xri:pqdiss&rft_dat=xri:pqdiss:6908427Google Scholar
35.Saracino, D., The 2-color Rado number of x 1 + x 2 + · · · + x n = y 1 + y 2 + · · · + y k, Ars Combin. 129 (2016), 315–321.Google Scholar
36.Schur, I., Über die Kongruenz x m + y m ≡ z m (mod.p), Jahresber. Dtsch. Math.-Ver. 25 (1916), 114–117.Google Scholar
37.Shkredov, I. D., Fourier analysis in combinatorial number theory, Russ. Math. Surv. 65(3) (2010), 513–567.CrossRefGoogle Scholar
38.Tao, T. C., Higher order Fourier analysis, Graduate Studies in Mathematics, Volume 142 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
39.Tao, T. C. and Vu, V. H., Additive combinatorics, Cambridge Studies in Advanced Mathematics, Volume 105 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
40.van der Waerden, B. L., Beweis einer Baudetschen Vermutung, Nieuw Arch. Wiskd., II. Ser. 15 (1927), 212–216.Google Scholar
41.Walker, A., Gowers norms control Diophantine inequalities, preprint (arXiv.org/abs/1703. 00885), 2018.Google Scholar
42.Wolf, J., Finite field models in arithmetic combinatorics – ten years on, Finite Fields Appl. 32 (2015), 233–274.CrossRefGoogle Scholar