Article contents
Bohr radius for Banach spaces on simply connected domains
Published online by Cambridge University Press: 03 November 2023
Abstract
Let 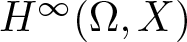 $H^{\infty}(\Omega,X)$ be the space of bounded analytic functions
$H^{\infty}(\Omega,X)$ be the space of bounded analytic functions 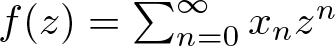 $f(z)=\sum_{n=0}^{\infty} x_{n}z^{n}$ from a proper simply connected domain Ω containing the unit disk
$f(z)=\sum_{n=0}^{\infty} x_{n}z^{n}$ from a proper simply connected domain Ω containing the unit disk 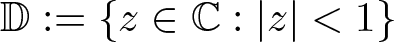 $\mathbb{D}:=\{z\in \mathbb{C}:|z| \lt 1\}$ into a complex Banach space X with
$\mathbb{D}:=\{z\in \mathbb{C}:|z| \lt 1\}$ into a complex Banach space X with 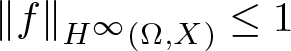 $\left\lVert f\right\rVert_{H^{\infty}(\Omega,X)} \leq 1$. Let
$\left\lVert f\right\rVert_{H^{\infty}(\Omega,X)} \leq 1$. Let 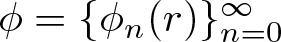 $\phi=\{\phi_{n}(r)\}_{n=0}^{\infty}$ with
$\phi=\{\phi_{n}(r)\}_{n=0}^{\infty}$ with 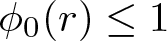 $\phi_{0}(r)\leq 1$ such that
$\phi_{0}(r)\leq 1$ such that 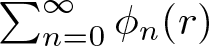 $\sum_{n=0}^{\infty} \phi_{n}(r)$ converges locally uniformly with respect to
$\sum_{n=0}^{\infty} \phi_{n}(r)$ converges locally uniformly with respect to 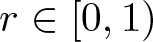 $r \in [0,1)$. For
$r \in [0,1)$. For 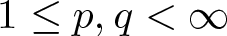 $1\leq p,q \lt \infty$, we denote
$1\leq p,q \lt \infty$, we denote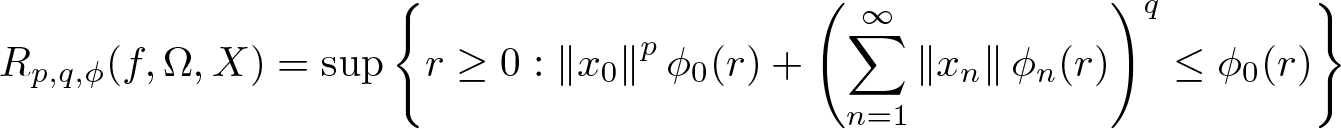 \begin{equation*}R_{p,q,\phi}(f,\Omega,X)= \sup \left\{r \geq 0: \left\lVert x_{0}\right\rVert^p \phi_{0}(r) + \left(\sum_{n=1}^{\infty} \left\lVert x_{n}\right\rVert\phi_{n}(r)\right)^q \leq \phi_{0}(r)\right\}\end{equation*}
\begin{equation*}R_{p,q,\phi}(f,\Omega,X)= \sup \left\{r \geq 0: \left\lVert x_{0}\right\rVert^p \phi_{0}(r) + \left(\sum_{n=1}^{\infty} \left\lVert x_{n}\right\rVert\phi_{n}(r)\right)^q \leq \phi_{0}(r)\right\}\end{equation*}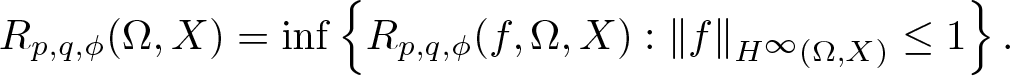 \begin{equation*}R_{p,q,\phi}(\Omega,X)=\inf \left\{R_{p,q,\phi}(f,\Omega,X): \left\lVert f\right\rVert_{H^{\infty}(\Omega,X)} \leq 1\right\}.\end{equation*}
\begin{equation*}R_{p,q,\phi}(\Omega,X)=\inf \left\{R_{p,q,\phi}(f,\Omega,X): \left\lVert f\right\rVert_{H^{\infty}(\Omega,X)} \leq 1\right\}.\end{equation*}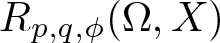 $R_{p,q,\phi}(\Omega,X)$, when X is an arbitrary Banach space, and
$R_{p,q,\phi}(\Omega,X)$, when X is an arbitrary Banach space, and 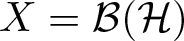 $X=\mathcal{B}(\mathcal{H})$ is the algebra of all bounded linear operators on a complex Hilbert space
$X=\mathcal{B}(\mathcal{H})$ is the algebra of all bounded linear operators on a complex Hilbert space 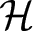 $\mathcal{H}$. Furthermore, we establish the Bohr inequality for the operator-valued Cesáro operator and Bernardi operator.
$\mathcal{H}$. Furthermore, we establish the Bohr inequality for the operator-valued Cesáro operator and Bernardi operator.
Keywords
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 1 , February 2024 , pp. 113 - 141
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
- 2
- Cited by



