Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barboza, Eudes Mendes
and
Ribeiro, Bruno
2023.
Elliptic systems of Hénon type involving one-sided critical growth.
Journal of Mathematical Analysis and Applications,
Vol. 517,
Issue. 1,
p.
126581.


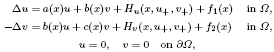
 and using variational methods, we prove the existence of two solutions depending on
and using variational methods, we prove the existence of two solutions depending on 