Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T03:41:30.030Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost Hermitian homogeneous structures

Published online by Cambridge University Press:  20 January 2009

Elsa Abbena  and
Sergio Garbiero
Elsa Abbena
Affiliation:
Dipartimento di MatematicaUniversità di Torino via Principe Amedeo, 8 10123 Torino, Italy
Sergio Garbiero
Affiliation:
Dipartimento di MatematicaUniversità di Torino via Principe Amedeo, 8 10123 Torino, Italy
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

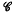Let (M, g, J) be an almost Hermitian manifold. More precisely, M is a ∞ differentiable manifold of dimension 2n, J is an almost complex structure on M, i.e. it is a tensor field of type (1, 1) such that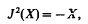

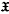for any X∈(M), (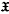(M) is the Lie algebra of 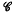∞ vector fields on M), and g is a Riemannian metric compatible with J, i.e.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 31 , Issue 3 , October 1988 , pp. 375 - 395
Copyright
Copyright © Edinburgh Mathematical Society 1988

References

REFERENCES

1.Abbena, E., An example of an almost Kähler manifold which is not Kählerian, Boll. Un. Mat. Ital. (6) (1984), 383–392.Google Scholar
2.Abbena, E. and Grassi, A., Hermitian left invariant metrics on complex Lie groups and cosymplectic Hermitian manifolds, Boll. Un. Mat. Ital. (6), 5-A (1986), 371–379.Google Scholar
3.Ambrose, W. and Singer, I. M., On homogeneous Riemannian manifolds, Duke Math. J. 25 (1958), 647–669.Google Scholar
4.Cordero, L. A., M. Fernandez and M. De Leon, Examples of compact non-Kähler almost Kähler manifolds, Proc. Amer. Math. Soc. 95 (1985), 280–286.Google Scholar
5.Cordero, L. A., Fernandez, M. and Gray, A., Symplectic manifolds with no Kähler structures, Topology 25 (1986), 375–380.Google Scholar
6.Deloff, E. D., Naturally reductive metrics and metrics with volume preserving geodesic symmetries on NC algebras (Ph.D. Thesis, The State University of New Jersey, 1979).Google Scholar
7.Gray, A., Nearly Kähler manifolds, J. Differential Geom. 4 (1970), 283–309.Google Scholar
8.Gray, A., Riemannian manifolds with geodesic symmetries of order 3, J. Differential Geom. 7 (1972), 343–369.CrossRefGoogle Scholar
9.Gray, A. and Hervella, L. M., The sixteen classes of almost Hermitian manifolds, Ann. Mat. Pura Appl. 123 (1980), 35–58.CrossRefGoogle Scholar
10.Kobayashi, S. and Nomizu, K., Foundations of differential geometry, Vol. I, II (Interscience Publ., New York, 1969).Google Scholar
11.Kowalski, O. and Tricerri, F., Riemannian manifolds of dimension≦4 admitting a homogeneous structure of type ⋯2, preprint.Google Scholar
12.Iwahori, N., Some remarks on tensors invariants of 0(n), U(n), Sp(n), J. Math. Soc. Japan 10 (1958), 143–160.CrossRefGoogle Scholar
13.Sekioawa, K., Notes on homogeneous almost Hermitian manifolds, Hokkaido Math. J. 7 (1978), 206–213.Google Scholar
14.Thurston, W. P., Some simple examples of symplectic manifolds, Proc. Amer. Math. Soc. 55 (1976), 467–468.Google Scholar
15.Tricerri, F., Varietà Riemanniane omogenee, Atti del Convegno Nazionale del GNSAGA del CNR, Torino 4–6 Ottobre 1984, 221–245.Google Scholar
16.Tricerri, F. and Vanhecke, L., Homogeneous structures on Riemannian manifolds (London Math. Soc. Lect. Notes 83, Cambridge Univ. Press, 1983).CrossRefGoogle Scholar
17.Tricerri, F. and Vanhecke, L., Special homogeneous structures on Riemannian manifolds, Proc. Colloq. Diff. Geom., Hajduszoboszlo (Debrecen, 1984), to appear.Google Scholar
18.Tricerri, F. and Vanhecke, L., Naturally reductive homogeneous spaces and Heisenberg groups, Compositio Math. 52 (1984), 389–408.Google Scholar
19.Tricerri, F. and Vanhecke, L., Curvature tensors on almost Hermitian manifolds, Trans. Amer. Math. Soc. 267 (1981), 365–398.CrossRefGoogle Scholar
20.Zwart, P. B. and Boothby, W. M., On compact homogeneous symplectic manifolds, Ann. Inst. Fourier (Grenoble) 30 (1980), 129–157.CrossRefGoogle Scholar