Article contents
Almost diagonal systems in asymptotic integration
Published online by Cambridge University Press: 20 January 2009
Extract
Consider the ordinary linear matrix differential system
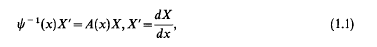
ψ(x) is a scalar mapping, X and A(x) are n by n matrices. Both belong to C1([a,∞)) for some integer l. The stability and asymptotic behaviour of its solutions have been subject to much investigation. See Bellman [2], Levinson [24], Hartman and Wintner [20], Devinatz [9], Fedoryuk [11], Harris and Lutz [16,17,18] and Cassell [30]. The special interest in eigenvalue problems and in the deficiency index problem stimulated a continued interest in asymptotic integration. See e.g. Naimark [36], Eastham and Grundniewicz [10] and [8,9]. Harris and Lutz [16,17,18] succeeded in explaining how to derive many known theorems in asymptotic integration by repeatedly using certain “(1 + Q)” linear transformations.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1985
References
REFERENCES
- 5
- Cited by


