Algebraic and Geometric Theory of the Topological Ring of Colombeau Generalized Functions

Abstract

We continue the investigation of the algebraic and topological structure of the algebra of Colombeau generalized functions with the aim of building up the algebraic basis for the theory of these functions. This was started in a previous work of Aragona and Juriaans, where the algebraic and topological structure of the Colombeau generalized numbers were studied. 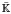Here, among other important things, we determine completely the minimal primes of and introduce several invariants of the ideals of 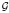(Ω). The main tools we use are the algebraic results obtained by Aragona and Juriaans and the theory of differential calculus on generalized manifolds developed by Aragona and co-workers. The main achievement of the differential calculus is that all classical objects, such as distributions, become C^∞-functions. Our purpose is to build an independent and intrinsic theory for Colombeau generalized functions and place them in a wider context.